Question

Draw a circle of radius \[4{\rm{ cm}}\]. Take a point P on the circle and construct a tangent to it.

Answer 1

Hint: This question is based on Geometry construction and we have to construct a circle of given radius and then draw a tangent on the circle using the centre of the circle. Now in order to draw the tangent on the circle we draw another circle with a radius less than the first circle by taking a point on the circumference of the first circle and then by using the theorem that “the tangent on a circle makes an angle of $90^\circ $ between the tangent and the line connecting the point at the circumference to the centre” we draw the tangent on the first circle.

Complete step-by-step answer:
Given:
The radius of the circle\[ = 4{\rm{ cm}}\].

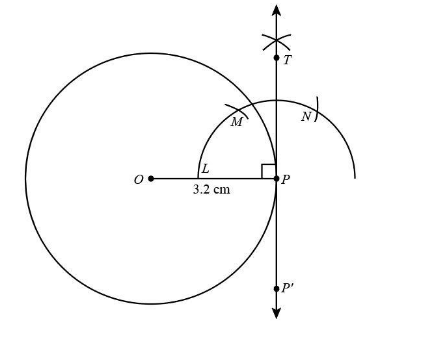
The step by step construction is given below:
(i) First take a radius of \[4{\rm{ cm}}\] using the ruler scale and draw a circle taking O as the centre of the circle.
(ii) Now take a point P on the circumference of the circle and then join OP.
(iii) Now take a radius less than the first circle and draw an arc of a circle taking point P as the centre of the arc, this arc intersects OP at a point L.
(iv) Taking LP as the radius draws an arc taking point L as the centre, this arc intersects the arc of the circle at point M.
(v) Now draw another arc with the same radius taking point M as the centre, this arc intersects the arc of the circle at point N.
(vi) Draw the bisector PT of the angle \[\angle MPN\].
(vi) Now extend the line segment TP to T'.
Therefore, the required tangent T'PT is constructed on a circle of radius \[4{\rm{ cm}}\].

Note: It should be noted that the bisector PT of the angle \[\angle MPN\] is always perpendicular to the line joining the contact point P and the centre of the circle O.
Which means that - $TP \bot OP$