Question

Draw a circle of radius \[4{\text{cm}}\]. Draw two tangents to the circle inclined at an angle of \[{60^0}\] to each other.

Answer 1

Hint: Here we will solve this problem by constructing two circles and by using the property of the equilateral triangle inside it which states that if a triangle is known as an equilateral triangle then, all the sides of that triangle are equal with all internal angles of \[{60^0}\]. We also know that the sum of the angles of any triangle is \[{180^0}\].

Complete step-by-step answer:
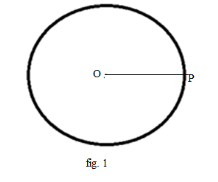
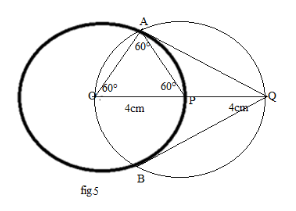
Step 1: We will construct a circle with a radius \[4{\text{cm}}\]from Centre O where \[{\text{OP}} = 4{\text{cm}}\]:

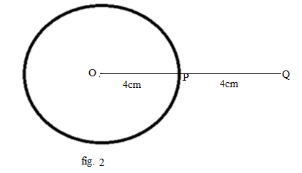
Step 2: Now, by extending
\[{\text{OP}}\]to a point \[{\text{Q}}\]in such a way that
\[{\text{OP}} = {\text{PQ = }}4{\text{cm}}\]:

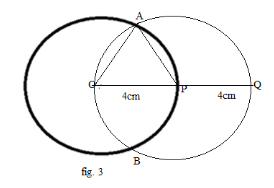
Step 3: By constructing a new circle with
\[{\text{P}}\]as a Centre and
\[{\text{PQ = }}4{\text{cm}}\] as a radius, which touches the other circle having Centre
\[{\text{O}}\] at points \[{\text{A}}\] and \[{\text{B}}\]:

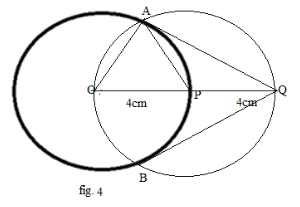
Step 4: Now in figure (4), by joining the points
\[{\text{AQ}}\] and \[{\text{BQ}}\] making the required tangents:

Step 5: Now in
\[\Delta {\text{OPA}}\] from fig. 4, we have:
\[{\text{OP}} = {\text{OA}} = 4{\text{cm}}\](
\[\because \]radii of the circle with Centre O)
Also,
\[{\text{AP = 4cm}}\] (\[\because \]radii of the circle with Centre P)
So, \[\Delta {\text{OPA}}\]will be an equilateral triangle and by using the property of the equilateral triangle having all the three sides equal. Also, in an equilateral triangle, all the three angles will be equal to \[{60^0}\].
\[ \Rightarrow \angle {\text{OAP}} = \angle {\text{APO}} = \angle {\text{AOP}} = {60^0}\]
Step 6:

Now, by using the property of the line segment that the sum of all angles on one side of a straight line is
\[{180^0}\] we have in the line segment OPQ sum of all angles will be \[{180^0}\]:
\[ \Rightarrow \angle {\text{APO + }}\angle {\text{APQ}} = {180^0}\]
By putting the value of
\[\angle {\text{APO}} = {60^0}\] in \[\angle {\text{APO + }}\angle {\text{APQ}} = {180^0}\] we get:
\[{60^0}{\text{ + }}\angle {\text{APQ}} = {180^0}\]
Thus, solving for \[\angle {\text{APQ}}\]
\[ \Rightarrow \angle {\text{APQ}} = {120^0}\]
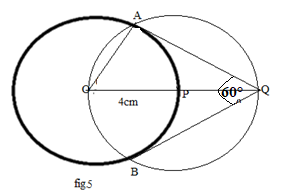
Step 7: Now, from fig. 5, in the
\[\Delta {\text{QPA}}\], we have:
\[{\text{PQ}} = {\text{PA}}\](
\[\because \]radii of the circle with Centre
\[{\text{P}}\]) and \[\angle {\text{APQ}} = {120^0}\]. Therefore,
\[\Delta {\text{QPA}}\] is an isosceles triangle.
By using the property of the isosceles triangle which states that if in any triangle two sides are equal then angles facing those sides will also be equal:
\[\angle {\text{AQP}} = \angle {\text{PAQ}}\]
Also, we know that the sum of a triangle always equal to
\[{180^0}\] so:
\[\angle {\text{APQ + }}\angle {\text{PAQ}} + \angle {\text{AQP}} = {180^0}\] …… (1)
Now by putting the value of
\[\angle {\text{APQ}} = {120^0}\] in the above equation (1), we get:
\[ \Rightarrow {\text{12}}{{\text{0}}^0}{\text{ + }}\angle {\text{PAQ}} + \angle {\text{AQP}} = {180^0}\]…………… (2)
Now, as we know that
\[\angle {\text{AQP}} = \angle {\text{PAQ}}\], by putting this in the above equation (2), we get:
\[ \Rightarrow {\text{12}}{{\text{0}}^0}{\text{ + }}\angle {\text{AQP}} + \angle {\text{AQP}} = {180^0}\] …….. (3)
Now by taking
\[{\text{12}}{{\text{0}}^0}\]on the RHS side and subtracting it by \[{180^0}\] in the above equation (3):
\[ \Rightarrow \angle {\text{AQP}} + \angle {\text{AQP}} = {60^0}\]
Now by adding the coefficient of
\[\angle {\text{AQP}}\]in the above equation, we get:
\[ \Rightarrow 2\angle {\text{AQP}} = {60^0}\]
By taking
\[2\] into the RHS side and dividing it:
\[ \Rightarrow \angle {\text{AQP}} = {30^0}\]
Step 8: Similarly, by repeating the same steps from step number (7) in
\[\Delta {\text{QPB}}\], we will calculate the value of
\[\angle {\text{BQP}}\] which will also equal
\[{30^0}\].
Now, by adding both of the angles
\[\angle {\text{AQP}}\]and
\[\angle {\text{BQP}}\] we get
\[\angle {\text{AQB}}\].
\[ \Rightarrow \angle {\text{AQP + }}\angle {\text{BQP = }}\angle {\text{AQB}}\]
By substituting the values of
\[\angle {\text{AQP}} = {30^0}\]and
\[\angle {\text{BQP}} = {30^0}\]in
\[\angle {\text{AQP + }}\angle {\text{BQP = }}\angle {\text{AQB}}\]we get:
\[ \Rightarrow {30^0}{\text{ + }}{30^0}{\text{ = }}\angle {\text{AQB}}\]
By adding in the LHS side we get our final answer:
\[ \Rightarrow \angle {\text{AQB = 6}}{{\text{0}}^0}\]
Thus, we get the required figure 5 where tangents are drawn to a circle inclined at an angle \[{60^0}\].

Note: If all the sides of a triangle are equal then the triangle is called equilateral triangle. If two sides of a triangle are equal and one side is not equal then it is called isosceles triangle.
You should always remember that Sum of the angle of any triangle always equals to
\[{180^0}\].