Draw a circle having radius $3 c m$ . Draw a chord XY $= 5 c m .$ Draw tangents at point X and Y without using centre.

Answer

Verified

483k+ views

Hint: For this construction we draw a chord of a circle of given length and join end points of chords with Centre and then at both ends draw an angle of

90^{0}

to have tangents at both ends.

Complete step-by-step answer:
We first open a compass of radius

3 c m

and draw a circle. Name its centre as ‘O’.

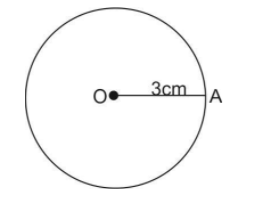
Now, we draw a chord of length 5cm and name it with initial X and Y. Join X and Y with the centre ‘O’ of the circle.

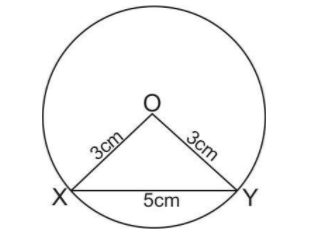
Now, to draw tangents at both initial X and Y. We draw an angle of

90^{0}

at initial X and Y both.

To draw an angle of

90^{0}

we just draw an arc of any radius at initial X and then with the same radius we just put two arcs and then on drawing bisectors of these two arcs give an angle of measurement

90^{0}

. Also repeat for initial Y.
These perpendicular lines are tangent lines at initial X and Y.

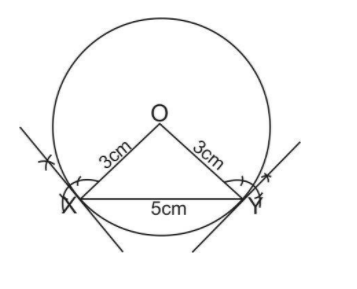
Which is the required construction of given measurements.

Note: A tangent to a circle is a straight line which touches the circle at only one point. This point is called the point of tangency. The tangent to a circle is perpendicular to the radius at the point of tangency.