
What is the domain and range of \[y=\dfrac{3}{x}\]?
Answer
527.1k+ views
Hint: We are given with \[y=\dfrac{3}{x}\] which means that it has a variable in the denominator. To compute the domain and range of a function with a variable in the denominator, we must set the denominator equal to zero and then we have to exclude \[x\], we get an equation to be solved.
Complete step by step solution:
Now let us have a brief regarding the range and domain of functions. The domain means the set of possible input values. The graph of a domain consists of all the values that are shown upon the \[x-axis\]. The range is nothing but the set of possible output values. The graph of range consists of values that are represented upon the \[y-axis\]. We can find the domain and range by using graphs since both of them contain the required values that are to be plotted.
Now let us start finding the domain \[y=\dfrac{3}{x}\].
While finding the domain, we shall not divide by \[0\] because it will give undefined value of y.
Since \[y\] is defined \[\forall x\in R:x\ne 0\]
\[R-\left\{ 0 \right\}\]
\[\therefore \]The domain of \[y=\dfrac{3}{x}\] would be \[\left( -\infty ,0 \right)\cup \left( 0,+\infty \right)\]
Now let us find the range of \[y=\dfrac{3}{x}\].
Let us consider that-
\[\begin{align}
& \underset{x>0-}{\mathop{\lim }}\,y=-\infty \\
& \underset{x<0+}{\mathop{\lim }}\,=+\infty \\
\end{align}\]
\[\therefore \] The range of \[y=\dfrac{3}{x}\] is \[\left( -\infty ,+\infty \right)\]
Note: The rule of the domain is that if a function contains a square root, we must set the equation inside the square root greater or equal to zero and solve. The resulting answer would be the domain. If the function contains a fraction, set the denominator not equal to zero. By solving this, we obtain the domain.
The graph of \[y=\dfrac{3}{x}\] is
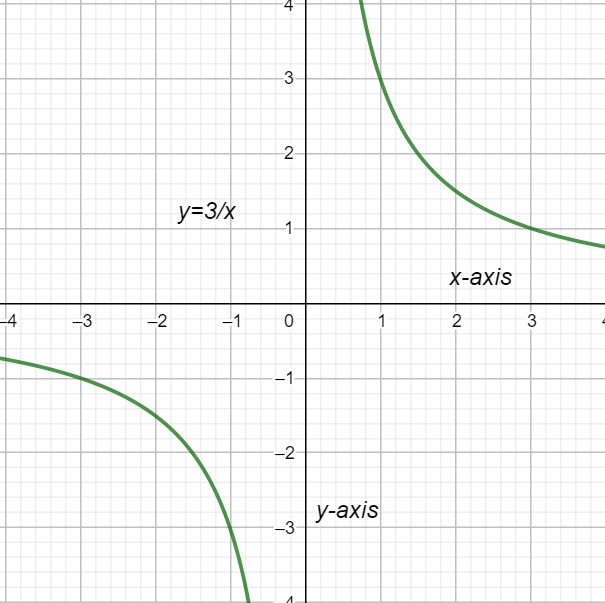
Complete step by step solution:
Now let us have a brief regarding the range and domain of functions. The domain means the set of possible input values. The graph of a domain consists of all the values that are shown upon the \[x-axis\]. The range is nothing but the set of possible output values. The graph of range consists of values that are represented upon the \[y-axis\]. We can find the domain and range by using graphs since both of them contain the required values that are to be plotted.
Now let us start finding the domain \[y=\dfrac{3}{x}\].
While finding the domain, we shall not divide by \[0\] because it will give undefined value of y.
Since \[y\] is defined \[\forall x\in R:x\ne 0\]
\[R-\left\{ 0 \right\}\]
\[\therefore \]The domain of \[y=\dfrac{3}{x}\] would be \[\left( -\infty ,0 \right)\cup \left( 0,+\infty \right)\]
Now let us find the range of \[y=\dfrac{3}{x}\].
Let us consider that-
\[\begin{align}
& \underset{x>0-}{\mathop{\lim }}\,y=-\infty \\
& \underset{x<0+}{\mathop{\lim }}\,=+\infty \\
\end{align}\]
\[\therefore \] The range of \[y=\dfrac{3}{x}\] is \[\left( -\infty ,+\infty \right)\]
Note: The rule of the domain is that if a function contains a square root, we must set the equation inside the square root greater or equal to zero and solve. The resulting answer would be the domain. If the function contains a fraction, set the denominator not equal to zero. By solving this, we obtain the domain.
The graph of \[y=\dfrac{3}{x}\] is

Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




