Question

What is the domain and range of $\cos \left( \dfrac{1}{x} \right)?$

Answer 1

Hint: Domain of a function can be defined as the set of all the valid input values for the function. Range of a function is the set of all the outputs obtained from the function by substituting the values of the domain in it. Using this, we first plot the graph of the function $\cos \left( \dfrac{1}{x} \right).$ The we see the set of values that qualify as its domain. Using this, we check for its range and represent that.

Complete step by step solution:
In order to solve this question, let us first plot the curve for the given function \[\cos \left( \dfrac{1}{x} \right).\] We obtain a graph as shown below.

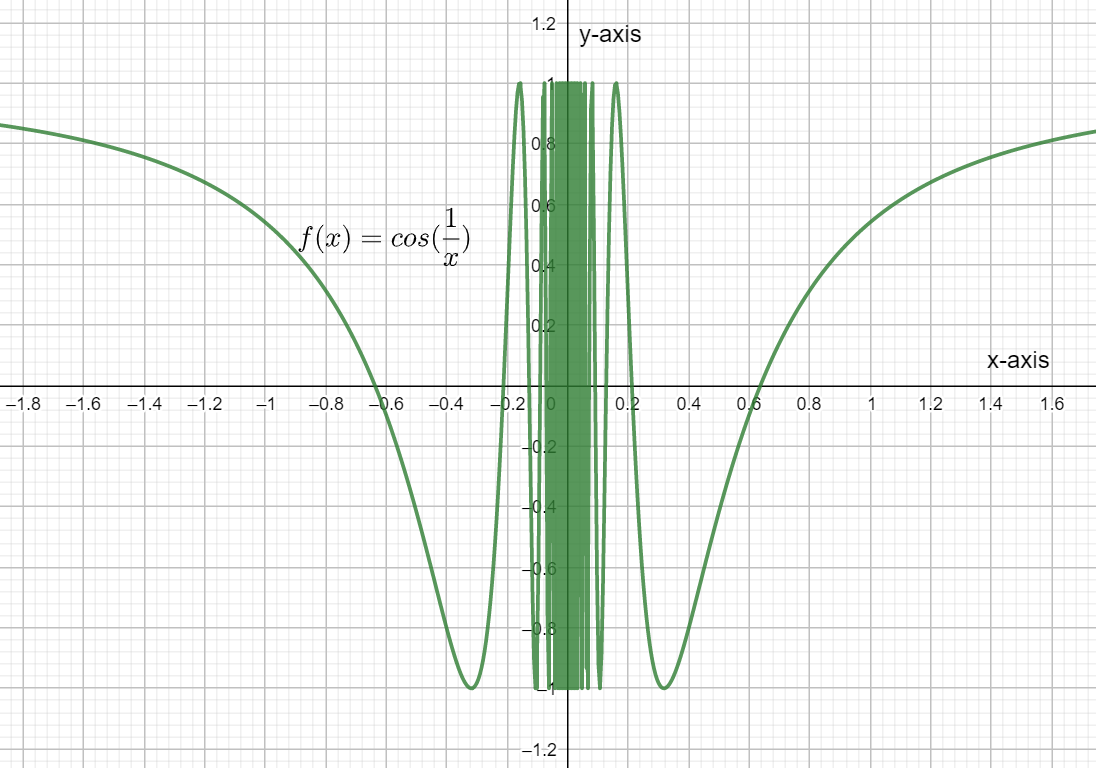
Let us consider the given function as $f\left( x \right)=\cos \left( \dfrac{1}{x} \right).$ As we can see in the graph, the function is defined for all values of x except at x=0. This can be shown as follows,
$\Rightarrow f\left( 0 \right)=\cos \left( \dfrac{1}{0} \right)=\cos \left( \infty \right)$
We know that $\cos \left( \infty \right)$ does not exist, so the domain of the function $f\left( x \right)$ can be given as $\left( -\infty ,0 \right)\bigcup \left( 0,\infty \right).$
To find out the range of the given function, we need to substitute the limiting values for the given function. We take the limits tending to positive and negative infinity and check its value.
$\Rightarrow \displaystyle \lim_{x \to +\infty }\cos \left( \dfrac{1}{x} \right)=\cos \left( 0 \right)=1$
$\Rightarrow \displaystyle \lim_{x \to -\infty }\cos \left( \dfrac{1}{x} \right)=\cos \left( -0 \right)=1$
We can see that as the x values tend to infinity on both sides, the value of the function is just 1. Also as seen from the graph the maximum output value of the function is $\pm 1.$ Hence, the range of the function $f\left( x \right)=\cos \left( \dfrac{1}{x} \right)$ is given by $\left[ -1,1 \right].$
Hence, the domain and range of the function $\cos \left( \dfrac{1}{x} \right)$ are $\left( -\infty ,0 \right)\bigcup \left( 0,\infty \right)$ and $\left[ -1,1 \right]$ respectively.

Note: We need to know the definition of domain and range and how to calculate them for solving such problems. We need to note that since the input for x=0 is not valid for the given function, the output at x=0 does not exist for the given function.