Question

How does the strength of an object’s electric field change with distance?

Answer 1

Hint: Electric field is defined as a space surrounding a charge in which another “static” charge experiences a force on it.
Strength or intensity of electric field at a point in a region where electric field is present can be defined as the force experienced by a unit charge placed at that point. The unit used for the measurement of the electric field strength is newton per coulomb or in short N/C.

Complete step by step answer:
When a charge is brought close to another fixed charge then it experiences some force on it due to the presence of the fixed charge. The region in the surrounding of a charge where any other charge experiences a force is called the electric field of the charge. In other words we can say that an electric field is the space surrounding an electric field q in which another charge q’ experiences an electrostatic force of attraction, or repulsion.

Determining the strength of the electric field strength:
If we wish to find the electric field strength at a point A which is located at a distance r from a fixed point charge Q, we have to place the unit positive charge at a distance r from the fixed one.

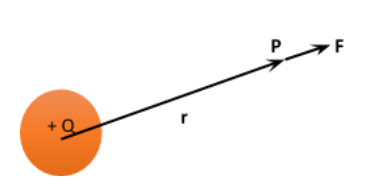
Now the electrostatic force on unit positive charge is given as:-
\[F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Q( + 1)}}{{{r^2}}}\]
i.e.
\[F = \dfrac{{KQ}}{{{r^2}}}\] ----(i)
The equation (i) gives the magnitude of electric field strength at the point P due to + q charge. Thus in order to determine the electric field at a point due to a point charge such as explained in above diagram, the force on +1C charge will give the desired result but if we want to calculate the electric field strength at a point due to distributed on a metal body, use of +1C charge at that point will change the distribution of charges on body because of charge induction on the body.

Note: For calculation of the electric field at a point in the surrounding of the extended charged bodies, the coulomb method discussed above is not appropriate.
Consider a situation as shown below:

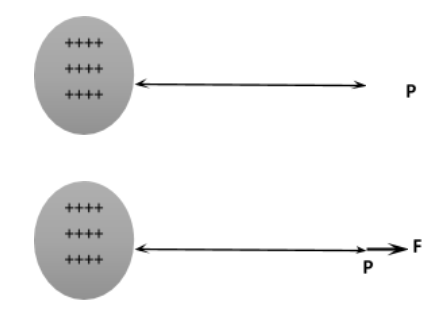
Now at point P we place a very small positive charge \[{q_0}\] as shown in above figure. This charge \[{q_0}\] is considered to be so small that it cannot produce any significant force on any charge on the body to charge distribution. Now if we find force on this charge due to the body, if it is F then the force per unit charge at the point P is given by :
\[{E_P} = \dfrac{F}{{{q_0}}}\]