Question

How far does the stick’s center of mass move during one rotation of the stick?

(A) $\dfrac{2}{3}\pi l$
(B) $\dfrac{5}{6}\pi l$
(C) $\dfrac{6}{5}\pi l$
(D) $\dfrac{5}{6}{\pi ^2}l$

Answer 1

Hint: This question uses the concept of conservation of angular momentum. Firstly you need to calculate the total angular momentum of the system before and after the collision. Also, you will be required to calculate the new center of mass of the system and its velocity. After applying the conservation of angular momentum, you will get an expression for angular velocity. Lastly, you need to apply the formula to find the distance using speed and time.

Complete step by step answer:
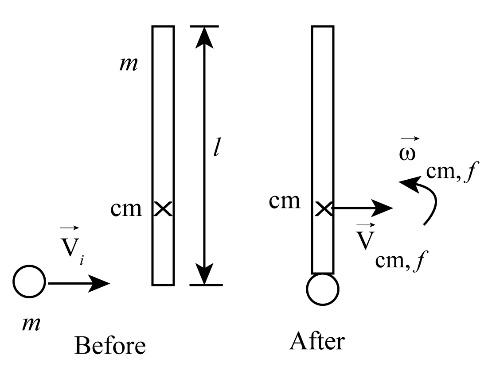
It is clear from the figure that, the length of the stick is l and the mass of the stick is m, mass of the ball is also m.

We know that the stick is stationary, its angular momentum will be zero.
The total angular momentum of the system (stick-ball) before the collision can be given as,
$
{L_1} = {r_p} + 0\\
\implies {L_1} = \dfrac{1}{4}m{v_i}......\left( 1 \right)
$
As we know that the stick is stationary, its angular momentum will be zero.

The new center of mass of the system (stick-ball) with respect to the center of the stick can be given as,
$
{r_{cm}} = \dfrac{{{m_s}\left( {\dfrac{d}{2}} \right)}}{{{m_s} + {m_p}}}\\
\implies {r_{cm}} = \dfrac{{m \times \left( {\dfrac{l}{2}} \right)}}{{m + m}}\\
\implies {r_{cm}} = \dfrac{l}{4}
$

(As it is given that mass of stick and ball is same)

We can calculate the velocity of the system as,
$
{v_{cm}} = \dfrac{{m{v_i}}}{{m + m}}\\
\implies {v_{cm}} = \dfrac{{{v_i}}}{2}......\left( 2 \right)
$

The total angular momentum of the system (stick-ball) after the collision can be given as,
${L_2} = {I'_{cm}}\omega ......\left( 3 \right)$
Here, ${I '_{cm}}$ is the moment of inertia of the system about the new center of mass.

On applying the law of conservation of angular momentum, we will get,
${L_1} = {L_2}$

Further, we substitute the values in above expression,
$
{{I'}_{cm}}\omega = \dfrac{1}{4}m{v_i}\\
\omega = \dfrac{{m{v_i}}}{{4{{I'}_{cm}}}}......\left( 4 \right)
$

As ${I'_{cm}}$ is the moment of inertia of the system, it can be written as,
${I'_{cm}} = {I_s} + {I_p}......\left( 5 \right)$

Now on applying parallel axis theorem, we get ${I_s} = {I_{cm}} + m{\left( {\dfrac{d}{4}} \right)^2}$ and ${I_p} = m{\left( {\dfrac{l}{4}} \right)^2}$.

Also, the moment of inertia of the stick is given as,
${I_{cm}} = m\left( {\dfrac{{{l^2}}}{{12}}} \right)$

So equation (5) can be written as,
$
{{I'}_{cm}} = {I_{cm}} + m{\left( {\dfrac{l}{4}} \right)^2} + m{\left( {\dfrac{l}{4}} \right)^2}\\
\implies {{I'}_{cm}} = m\left( {\dfrac{{{l^2}}}{{12}}} \right) + m\left( {\dfrac{{{l^2}}}{8}} \right)\\
\implies {{I'}_{cm}} = m\left( {\dfrac{{5{l^2}}}{{24}}} \right)
$

We substitute the values in equation (5),
$
\omega = \dfrac{{m{v_i}}}{{4{{I'}_{cm}}}}\;\\
\implies \omega = \dfrac{{m{v_i}}}{{4m\left( {\dfrac{{5{l^2}}}{{24}}} \right)}}\\
\implies \omega = \dfrac{{6{v_i}}}{{5l}}
$

We can calculated the distance travelled by center of mass in one rotation as,
$
d = {v_{cm}}T\\
\implies d = \dfrac{{{v_i}}}{2} \times \dfrac{{2\pi }}{\omega }\\
\implies d = {v_i} \times \dfrac{{2\pi }}{{\dfrac{{6{v_i}}}{{5l}}}}\\
\therefore d = \dfrac{{5\pi l}}{6}
$
So, the center of mass of the stick moves $\dfrac{{5\pi l}}{6}$ during one rotation.

Thus, option (B) is correct.

Note:
Make sure that you calculate the individual angular momentum of the system correctly. Make sure that you substitute one expression into another correctly, or else you will get the wrong answer.