Question

What does the equation $9{{y}^{2}}-4{{x}^{2}}=36$ tell me about its hyperbola?

Answer 1

Hint: For solving this question you should know about the concept of hyperbola. And you should know about the equations of hyperbola and to find the axis of hyperbola, coordinate of foci, coordinate of vertices, eccentricity of a hyperbola and the latus rectum of the hyperbola. The equation of a hyperbola tells us everything about all of these elements of the hyperbola.

Complete step-by-step solution:
According to our question the equation of a hyperbola is $9{{y}^{2}}-4{{x}^{2}}=36$. Simply we can say that a hyperbola is a symmetrical open curve which is formed by the intersection of a circular cone with a plane at any small angle with its axis than the sides of a cone. All the elements of a hyperbola are shown in the figure below.

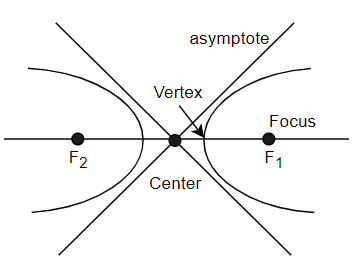
According to our equation, if we see that;
Then $9{{y}^{2}}-4{{x}^{2}}=36$
Divide the whole equation by 36,
$\begin{align}
  & \Rightarrow \dfrac{9{{y}^{2}}}{36}-\dfrac{4{{x}^{2}}}{36}=\dfrac{36}{36} \\
 & \Rightarrow \dfrac{{{y}^{2}}}{4}-\dfrac{{{x}^{2}}}{9}=1\ldots \ldots \ldots \left( 1 \right) \\
\end{align}$
So, the equation of the hyperbola is $\dfrac{{{y}^{2}}}{4}-\dfrac{{{x}^{2}}}{9}=1$.
It will be the y-axis of this hyperbola.
For the coordinates of Foci,
$\begin{align}
  & {{c}^{2}}={{a}^{2}}+{{b}^{2}} \\
 & \Rightarrow {{c}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 3 \right)}^{2}} \\
 & \Rightarrow {{c}^{2}}=4+9=13 \\
 & \Rightarrow c=\sqrt{13} \\
\end{align}$
So, the coordinate of Foci $=\left( 0,\pm c \right)=\left( 0,\pm \sqrt{13} \right)$.
So, the Foci are $\left( 0,\sqrt{13} \right)$ and $\left( 0,-\sqrt{13} \right)$.
Coordinates of the vertices $=\left( 0,\pm a \right)=\left( 0,\pm 2 \right)$.
So, the coordinates of the vertices are $\left( 0,2 \right)$ and $\left( 0,-2 \right)$.
Eccentricity of the hyperbola $=e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{2}$.
And the latus rectum of the hyperbola $=\dfrac{2{{b}^{2}}}{2}=\dfrac{2\times 9}{2}=2$.
Thus, the equation of the hyperbola shows everything like this.

Note: The equation of a hyperbola is always in $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ form if the axis of hyperbola is x-axis and it will be in the form of $\dfrac{{{y}^{2}}}{{{a}^{2}}}-\dfrac{{{x}^{2}}}{{{b}^{2}}}=1$ if the axis of the hyperbola is y-axis and the coordinates of Foci and coordinates of vertex will also change respectively. And eccentricity and latus rectum will remain the same.