Question

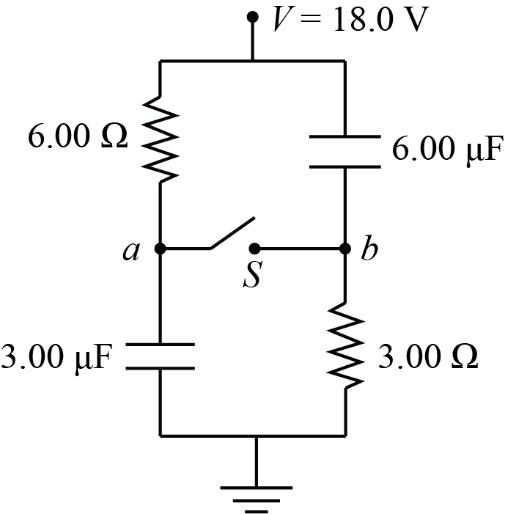
How much does the charge on each capacitor change when $S$ is closed?

Answer 1

Hint: The voltage across capacitors will be different when the switch is closed and not closed. We will use the equation connecting charge, voltage and capacitance to find the charge on capacitors.

Complete step by step answer:
For a better understanding, first let us define the values given in the circuit.
Let the given resistances ${R_{6\;\Omega }} = 6\;\Omega $, ${R_{3\;\Omega }} = 3\;\Omega $,
Capacitance of capacitors,${C_{6\;{\rm{\mu F}}}} = 6\;{\rm{\mu F}}$, ${C_{3\;{\rm{\mu F}}}} = 3\;{\rm{\mu F}}$
Voltage supplied, $V = 18\;{\rm{V}}$

First let us find the current flowing through the resistors ${R_{6\;\Omega }}$ and ${R_{3\;\Omega }}$. The current is given by,
$I = \dfrac{V}{{{R_{6\;\Omega }} + {R_{3\;\Omega }}}}$
Substituting the values of $V$, ${R_{6\;\Omega }}$ and ${R_{3\;\Omega }}$ in the above equation, we ge
$\begin{array}{c}
I = \dfrac{{18}}{{6 + 3}}\\
 = 2\;{\rm{A}}
\end{array}$

When the switch $S$ is not closed, the voltage ${V_{6\;{\rm{\mu F}}}}$ across ${C_{6\;{\rm{\mu F}}}}$ and the voltage ${V_{3\;{\rm{\mu F}}}}$ across ${C_{3\;{\rm{\mu F}}}}$ is $18\;{\rm{V}}$ itself. Hence,
${V_{6\;{\rm{\mu F}}}} = {V_{3\;{\rm{\mu F}}}} = 18\;{\rm{V}}$

Now, we can express the charge across the $6\;{\rm{\mu F}}$ capacitor as
${Q_{6\;{\rm{\mu F}}}} = {C_{6\;{\rm{\mu F}}}}{V_{6\;{\rm{\mu F}}}}$

Substituting the values for ${C_{6\;{\rm{\mu F}}}}$ and ${V_{6\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
{Q_{6\;{\rm{\mu F}}}} = 6 \times 18\\
 = 108\,{\rm{\mu C}}
\end{array}$

We can express the charge across the $3\;{\rm{\mu F}}$ capacitor as
${Q_{3\;{\rm{\mu F}}}} = {C_{3\;{\rm{\mu F}}}}{V_{3\;{\rm{\mu F}}}}$

Substituting the values for ${C_{3\;{\rm{\mu F}}}}$ and ${V_{3\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
{Q_{3\;{\rm{\mu F}}}} = 3 \times 18\\
 = 54\;{\rm{\mu C}}
\end{array}$

When the switch $S$ is closed, the voltage drop across $6\;{\rm{\mu F}}$ capacitor will be equal to the voltage drop across ${R_{6\;\Omega }} = 6\;\Omega $.
${V_{6\;{\rm{\mu F}}}} = {V_{6\Omega }}$

Now, the voltage drop across ${R_{6\;\Omega }} = 6\;\Omega $ can be written as
${V_{6\Omega }} = I{R_{6\Omega }}$

Substituting the values of $I$ and ${R_{6\;\Omega }}$, we get
$\begin{array}{c}
{V_{6\Omega }} = 2 \times 6\\
 = 12\;{\rm{V}}
\end{array}$
Hence, ${V_{6\;{\rm{\mu F}}}} = 12\;{\rm{V}}$

Now, the new charge across ${C_{6\;{\rm{\mu F}}}} = 6\;{\rm{\mu F}}$ can be written as
${q_{6\;{\rm{\mu F}}}} = {C_{6\;{\rm{\mu F}}}}{V_{_{6\;{\rm{\mu F}}}}}$

Substituting the values of ${C_{6\;{\rm{\mu F}}}}$ and ${V_{6\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
{q_{6\;{\rm{\mu F}}}} = 6 \times 12\\
 = 72\;{\rm{\mu C}}
\end{array}$

Similarly, when the switch $S$ is closed, the voltage drop across $3\;{\rm{\mu F}}$ capacitor will be equal to the voltage drop across ${R_{3\;\Omega }} = 3\;\Omega $.
${V_{3\;{\rm{\mu F}}}} = {V_{3\Omega }}$

Now, the voltage drop across ${R_{3\;\Omega }} = 3\;\Omega $ can be written as
${V_{3\Omega }} = I{R_{3\Omega }}$

Substituting the values of $I$ and ${R_{3\;\Omega }}$, we get
$\begin{array}{c}
{V_{3\Omega }} = 2 \times 3\\
 = 6\;{\rm{V}}
\end{array}$
Hence, ${V_{3\;{\rm{\mu F}}}} = 6\;{\rm{V}}$

Now, the new charge across ${C_{3\;{\rm{\mu F}}}} = 3\;{\rm{\mu F}}$ can be written as
\[{q_{3\;{\rm{\mu F}}}} = {C_{3\;{\rm{\mu F}}}}{V_{{\rm{3}}\;{\rm{\mu F}}}}\]

Substituting the values of ${C_{3\;{\rm{\mu F}}}}$ and ${V_{3\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
{q_{3\;{\rm{\mu F}}}} = 3 \times 6\\
 = 18\;{\rm{\mu C}}
\end{array}$

Now, the change in the charge of ${\rm{16}}\;{\rm{\mu F}}$ capacitor after the switch is closed can be written as
$\Delta {Q_{{\rm{6}}\;{\rm{\mu F}}}} = {q_{6\;{\rm{\mu F}}}} - {Q_{6\;{\rm{\mu F}}}}$

Substituting ${\rm{78}}\;{\rm{\mu C}}$ for ${q_{6\;{\rm{\mu F}}}}$ and $108\;{\rm{\mu C}}$ for ${Q_{6\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
\Delta {Q_{{\rm{6}}\;{\rm{\mu F}}}} = 78 - 108\\
 = - 36\;{\rm{\mu C}}
\end{array}$

Again, the change in the charge of $3\;{\rm{\mu F}}$ capacitor after the switch is closed can be written as
$\Delta {Q_{3\;{\rm{\mu F}}}} = {q_{3\;{\rm{\mu F}}}} - {Q_{3\;{\rm{\mu F}}}}$

Substituting $18\;{\rm{\mu C}}$ for ${q_{3\;{\rm{\mu F}}}}$ and $54\;{\rm{\mu C}}$ for ${Q_{3\;{\rm{\mu F}}}}$, we get
$\begin{array}{c}
\Delta {Q_{3\;{\rm{\mu F}}}} = 18 - 54\\
 = - 36\;{\rm{\mu C}}
\end{array}$

Therefore, the change in charge on both the capacitors is $ - 36\;{\rm{\mu C}}$.

Note:
It should be noted that one end of the circuit is connected to the ground. Since the potential of the ground is always zero, we took the potential difference as $18\;{\rm{V}}$ itself in calculations when the switch is not closed.