Question

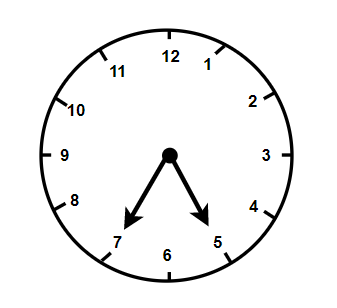
What does the angle made by the hour hand of the clock look like when it moves from $5$ to $7$ . Is the angle moved more than $1$ right angle?

Answer 1

Hint: For solving this type of question we should know about the angles between two consecutive minutes. As we know that the complete revolution in one cycle is equal to ${360^0}$ . So by using this we will calculate the angle between two numbers and hence then we will have the angle made between $5$ to $7$ .

Complete step-by-step answer:
As we can see the clock includes the number from $1$ to $12$ and are equally spaced on the boundary of the circle or we can say on the circumference of the clock.
Therefore, the angle made between the two numbers will be given by
$ \Rightarrow \dfrac{{360}}{{12}}$
And on solving it, we get the number as
$ \Rightarrow {30^ \circ }$
Hence, the angle made by the hour hand while it is moving from $5$ to $7$ will be ${60^ \circ }$.
And we also then said that for the right angle the angle should be ${90^ \circ }$ .
Hence, the degree we get from the clock will not be more than the right angle.

Note: So for finding the angle between the hands of a clock is easy as long as we don’t use the time which is a little bit complicated. For solving and finding those degrees we need to know the geometry and also how we are able to reach that quarter in the clock. Also, we should know that at six o clock the hands of the clock will lie in a straight line and so it will make an angle of ${180^ \circ }$ between them. So we should not answer the time $9:15$ as at this time the angle is not exactly ${30^ \circ }$ .