
How does one derive the Midpoint formula?
Answer
552k+ views
Hint: Here, we will consider two points in a straight line and a midpoint of the two points. Then by using the equality of vectors, we will equate the vectors. Again, by subtracting the coordinates of the vector to find the distance between the points and by equating both the distance, we will get the coordinates of the midpoint.
Complete step by step solution:
Let \[A\] and \[B\] be two points in a straight line. Let \[A\left( {{x_A},{y_A}} \right)\] and \[B\left( {{x_B},{y_B}} \right)\] be the coordinates of the Points in a straight line.
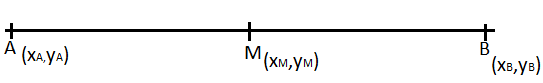
Let us consider a point \[M\] which is at the equidistant from both the points \[A\] and\[B\]. So \[M\] is the midpoint of a straight line. Let the coordinates of \[M\] be \[\left( {{x_M},{y_M}} \right)\].
Now, we will use the vectors to derive the midpoint formula.
Since \[A\] and \[B\] are equidistant from the midpoint \[M\], we get \[\overrightarrow {AM} \] and\[\overrightarrow {BM} \] are equal.
Now, by using the equality of vectors , we get
\[\overrightarrow {AM} = \overrightarrow {BM} \]
Now, by subtracting the coordinates for the given vectors, we get
\[ \Rightarrow \left( {{x_M} - {x_A},{y_M} - {y_A}} \right) = \left( {{x_B} - {x_M},{y_B} - {y_M}} \right)\]
Now, by equating the \[x\] - coordinates, we get
\[ \Rightarrow {x_M} - {x_A} = {x_B} - {x_M}\]
Rewriting the equation, we get
\[ \Rightarrow {x_M} + {x_M} = {x_B} + {x_A}\]
Adding the terms, we get
\[ \Rightarrow 2{x_M} = {x_B} + {x_A}\]
Dividing both sides by 2, we get
\[ \Rightarrow {x_M} = \dfrac{{{x_A} + {x_B}}}{2}\] ………………………………………………………………\[\left( 1 \right)\]
Now, by equating the \[y\] - coordinates, we get
\[{y_M} - {y_A} = {y_B} - {y_M}\]
Rewriting the equation, we get
\[ \Rightarrow {y_M} + {y_M} = {y_B} + {y_A}\]
Adding the terms, we get
\[ \Rightarrow 2{y_M} = {y_B} + {y_A}\]
Dividing both sides by 2, we get
\[ \Rightarrow {y_M} = \dfrac{{{y_A} + {y_B}}}{2}\] ………………………………………………………………\[\left( 2 \right)\]
Thus, from equation \[\left( 1 \right)\] and \[\left( 2 \right)\] the coordinate of \[M\left( {{x_M},{y_M}} \right)\] be \[\left( {\dfrac{{{x_A} + {x_B}}}{2},\dfrac{{{y_A} + {y_B}}}{2}} \right)\].
Therefore, the midpoint formula \[\left( {\dfrac{{{x_A} + {x_B}}}{2},\dfrac{{{y_A} + {y_B}}}{2}}
\right)\] is derived.
Note:
We know that a vector is an object which has both a magnitude and a direction. When subtracting the vectors, we should always be careful that the tail vector should be subtracted from the head vector. Midpoint is defined as a point which is half way from the initial point. We will use the midpoint formula to find the midpoint of a line segment with two points. Midpoint formula is the representation of points using the coordinate system.
Complete step by step solution:
Let \[A\] and \[B\] be two points in a straight line. Let \[A\left( {{x_A},{y_A}} \right)\] and \[B\left( {{x_B},{y_B}} \right)\] be the coordinates of the Points in a straight line.
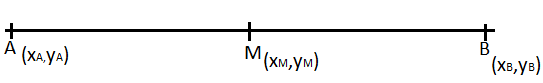
Let us consider a point \[M\] which is at the equidistant from both the points \[A\] and\[B\]. So \[M\] is the midpoint of a straight line. Let the coordinates of \[M\] be \[\left( {{x_M},{y_M}} \right)\].
Now, we will use the vectors to derive the midpoint formula.
Since \[A\] and \[B\] are equidistant from the midpoint \[M\], we get \[\overrightarrow {AM} \] and\[\overrightarrow {BM} \] are equal.
Now, by using the equality of vectors , we get
\[\overrightarrow {AM} = \overrightarrow {BM} \]
Now, by subtracting the coordinates for the given vectors, we get
\[ \Rightarrow \left( {{x_M} - {x_A},{y_M} - {y_A}} \right) = \left( {{x_B} - {x_M},{y_B} - {y_M}} \right)\]
Now, by equating the \[x\] - coordinates, we get
\[ \Rightarrow {x_M} - {x_A} = {x_B} - {x_M}\]
Rewriting the equation, we get
\[ \Rightarrow {x_M} + {x_M} = {x_B} + {x_A}\]
Adding the terms, we get
\[ \Rightarrow 2{x_M} = {x_B} + {x_A}\]
Dividing both sides by 2, we get
\[ \Rightarrow {x_M} = \dfrac{{{x_A} + {x_B}}}{2}\] ………………………………………………………………\[\left( 1 \right)\]
Now, by equating the \[y\] - coordinates, we get
\[{y_M} - {y_A} = {y_B} - {y_M}\]
Rewriting the equation, we get
\[ \Rightarrow {y_M} + {y_M} = {y_B} + {y_A}\]
Adding the terms, we get
\[ \Rightarrow 2{y_M} = {y_B} + {y_A}\]
Dividing both sides by 2, we get
\[ \Rightarrow {y_M} = \dfrac{{{y_A} + {y_B}}}{2}\] ………………………………………………………………\[\left( 2 \right)\]
Thus, from equation \[\left( 1 \right)\] and \[\left( 2 \right)\] the coordinate of \[M\left( {{x_M},{y_M}} \right)\] be \[\left( {\dfrac{{{x_A} + {x_B}}}{2},\dfrac{{{y_A} + {y_B}}}{2}} \right)\].
Therefore, the midpoint formula \[\left( {\dfrac{{{x_A} + {x_B}}}{2},\dfrac{{{y_A} + {y_B}}}{2}}
\right)\] is derived.
Note:
We know that a vector is an object which has both a magnitude and a direction. When subtracting the vectors, we should always be careful that the tail vector should be subtracted from the head vector. Midpoint is defined as a point which is half way from the initial point. We will use the midpoint formula to find the midpoint of a line segment with two points. Midpoint formula is the representation of points using the coordinate system.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Find the mode and median of the data 13 16 12 14 1-class-9-maths-CBSE

What were the main changes brought about by the Bolsheviks class 9 social science CBSE

What is the theme or message of the poem The road not class 9 english CBSE

What are the major achievements of the UNO class 9 social science CBSE

Explain the importance of pH in everyday life class 9 chemistry CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE




