
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Answer
596.4k+ views
Hint: Here, we will first use that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles and then prove it by using the graph and angles.
Complete step-by-step answer:
We know that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
It says that if \[\angle 1 + \angle 2 < 180^\circ \], the line \[a\] and \[b\] meet on the right side of line \[c\].
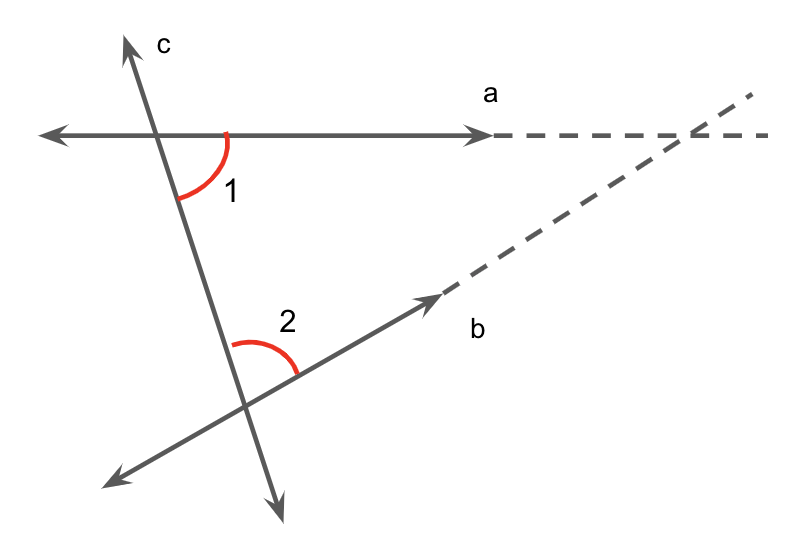
Therefore, by Euclid’s fifth postulate, line \[a\] and \[b\] will not meet on the right side of \[c\] as sum is not less than \[180^\circ \] as sum is not less than 180 degrees.
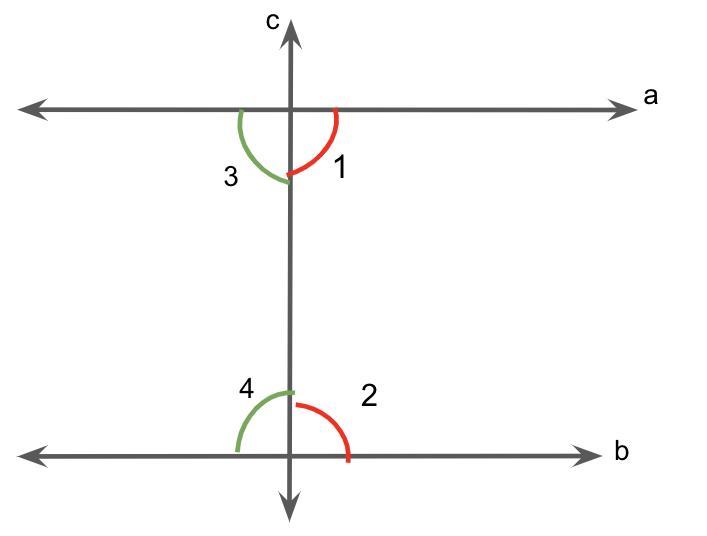
Similarly, we have \[\angle 3 + \angle 4 = 180^\circ \].
Hence, by Euclid’s fifth postulate, line \[a\] and \[b\] will not meet on the left side of \[c\] as sum is not less than \[180^\circ \] as sum is not less than 180 degrees.
Thus, Euclid’s postulate implies the existence of parallel lines.
Note: While solving these types of questions, students should know that a statement is an axiom, which is taken to be true without proof and postulates are the basic structure from which lemmas and theorems are derived. We need to know about the Euclid’s postulates before finding the solution of the problem.
Complete step-by-step answer:
We know that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
It says that if \[\angle 1 + \angle 2 < 180^\circ \], the line \[a\] and \[b\] meet on the right side of line \[c\].

Now since we know that \[a\] and \[b\] are parallel, then \[\angle 1 + \angle 2 = 180^\circ \], we have

Therefore, by Euclid’s fifth postulate, line \[a\] and \[b\] will not meet on the right side of \[c\] as sum is not less than \[180^\circ \] as sum is not less than 180 degrees.
Similarly, we have \[\angle 3 + \angle 4 = 180^\circ \].
Hence, by Euclid’s fifth postulate, line \[a\] and \[b\] will not meet on the left side of \[c\] as sum is not less than \[180^\circ \] as sum is not less than 180 degrees.
Thus, Euclid’s postulate implies the existence of parallel lines.
Note: While solving these types of questions, students should know that a statement is an axiom, which is taken to be true without proof and postulates are the basic structure from which lemmas and theorems are derived. We need to know about the Euclid’s postulates before finding the solution of the problem.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Write a letter to the editor of a newspaper explaining class 10 english CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?




