Question

How does change in the slope affect the steepness of a line?

Answer 1

Hint: We recall the slope-intercept equation of line that is $y=mx+c$ and the steepness of a line absolute value of the slope. We take different values of $m$ and see how the steepness of the line increases or decreases.

Complete step by step answer:
We know from the Cartesian coordinate system that every linear equation can be represented as a line. If the line is inclined with positive $x-$axis at an angle $\theta $ then its slope is given by $m=\tan \theta $ and of it cuts $y-$axis at a distance $c$ from the origin the intercept is given by $c$. The slope-intercept form of equation is given by
\[y=mx+c\]
The slope $m$ here means the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line.

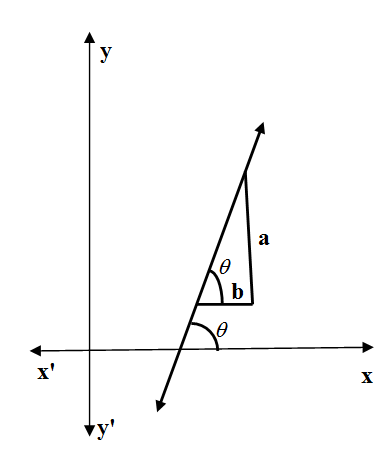
We also know that the steepness, incline, or grade of a line is measured by the absolute value of the slope which means$\left| m \right|$. A slope with a greater absolute value indicates a steeper line.
The positive values of slope indicates the angle of inclination $\theta $ is acute because $\tan \theta >0$ for $\theta \in \left( 0,\dfrac{\pi }{2} \right)$ and negative slope indicates angle of inclination $\theta $ is obtuse because $\tan \theta >0$ for $\theta \in \left( 0,\dfrac{\pi }{2} \right)$ . The positive or negative value of slope does not affect steepness as $m$ increases $\left| m \right|$ increases. If $m=0$ we get a line without steepness which is parallel to the $x-$axis and if $m=\infty $ we get the steepest line which is perpendicular to the $x-$axis.

Note:
We note that the slope is also called a rise over run which means to what extent and orientation is the line inclined with a positive $x-$axis. Steepness considers only inclination line not the orientation of line. The steepness is used to relay traffic warning signs in roads passing through mountains.