Question

why does amplitude of a vibrating body continuously decrease during damped vibrations?

Answer 1

Hint: If a body is vibrating continuously the surrounding medium plays a significant role in decreasing the amplitude due to external forces acting on it. During the vibrations external forces act opposite to direction of motion and exerts resistance force continuously.

Complete solution:
We know that the total energy of a harmonic oscillator remains constant in ideal conditions with constant amplitude and frequency and we call it a simple harmonic which can oscillate indefinitely without loss of amplitude and is also called undamped.

But the ideal conditions differs in very much extent from undamped oscillation because of external factors, observations states that when a body is freely oscillating the energy gradually decreases with time and oscillator can eventually comes to rest after some time, the main reason behind it is the presence of resistance from the surrounding which can be considered as frictional or damping force acting opposite to the motion leading to energy loss from the system.

For example, the vibrations from a tuning fork gradually decrease with time because in ideal physical conditions friction or damping force is always present to oppose the vibrations of tuning fork.

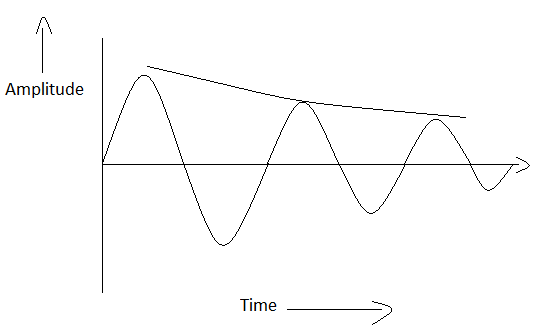
But, friction is not the only reason for loss of energy radiation plays a specific role as well, when an tuning fork is vibrating it imparts periodic motion to the particles of the medium and sound waves are produced by the radiation from the oscillator (:-refer electromagnetic waves from oscillating electric and magnetic field) which results in decrease in energy.

The direction of damping force is opposite to the motion of the body and directly proportional to the velocity of the body, and it is denoted by ${{F}_{d}}$
${{F}_{d}}=-pV$

Here, $V$ is the velocity of an object and $p$ is the viscous damping coefficient (damping force per unit velocity).

Note:
In many cases energy can be lost due to imperfect elasticity or internal factor of material, that’s why damping of a real system is considered as a complex phenomenon with many forces act simultaneously so sometimes it’s very difficult to predict the correct damping factors acting on the vibrating body which leads to loss in energy of the system.