Question

Why does ammonia have 4 shells that are $ s{p^3} $ hybridized, rather than having the s-shell for the non-bonding electron pair and the remaining 3 p-shells used for the covalent bonding with the hydrogen atoms?

Answer 1

Hint: Orbital hybridisation means the mixing of orbitals to form new hybrid orbitals with different energies, shapes and properties than their parent orbitals, which are suitable for forming chemical bonds in valence bond theory. In this question we will study the importance of hybridisation for the formation of compounds.

Complete answer:
In ammonia all the three hydrogens are identical and a lone pair is present on nitrogen, therefore it needs four identical orbitals to bond.
Suppose, there was no hybridisation and we have one s orbital with a lone pair and three p orbitals to hold the N-H bonding electron pairs. In that case all the three hydrogens will be aligned in the direction of their cartesian planes. Its $ 2{p_x} $ will be aligned to the x-axis, $ 2{p_y} $ and $ 2{p_z} $ to the y and z axis respectively. Ammonia is a three-dimensional molecule and will require hybridisation to make its bonds. If the bonds are aligned to the respective cartesian axes, we won’t be able to form a three-dimensional molecule, as the bonds couldn’t move off their cartesian axes. If the p orbitals move from their axes, they would no longer be pure orbitals. If a pure orbital re-aligns itself to a different axis, it will become a different orbital.
One major advantage of hybridisation is that it allows the directional p orbitals to lie on different axes by summing their vector directions. For $ s{p^3} $ we will hybridise four orbitals, one s and 3 p orbitals, we get:
 $ \overrightarrow {2s} + \overrightarrow {2{p_x}} + \overrightarrow {2{p_y}} + \overrightarrow {2{p_z}} = \left\langle {\overbrace 1^x,\overbrace 1^y,\overbrace 1^z} \right\rangle $
This is a three-dimensional vector and can be freely rotated in any direction and be valid under the quantum mechanical restrictions. Hence the shape of ammonia is:

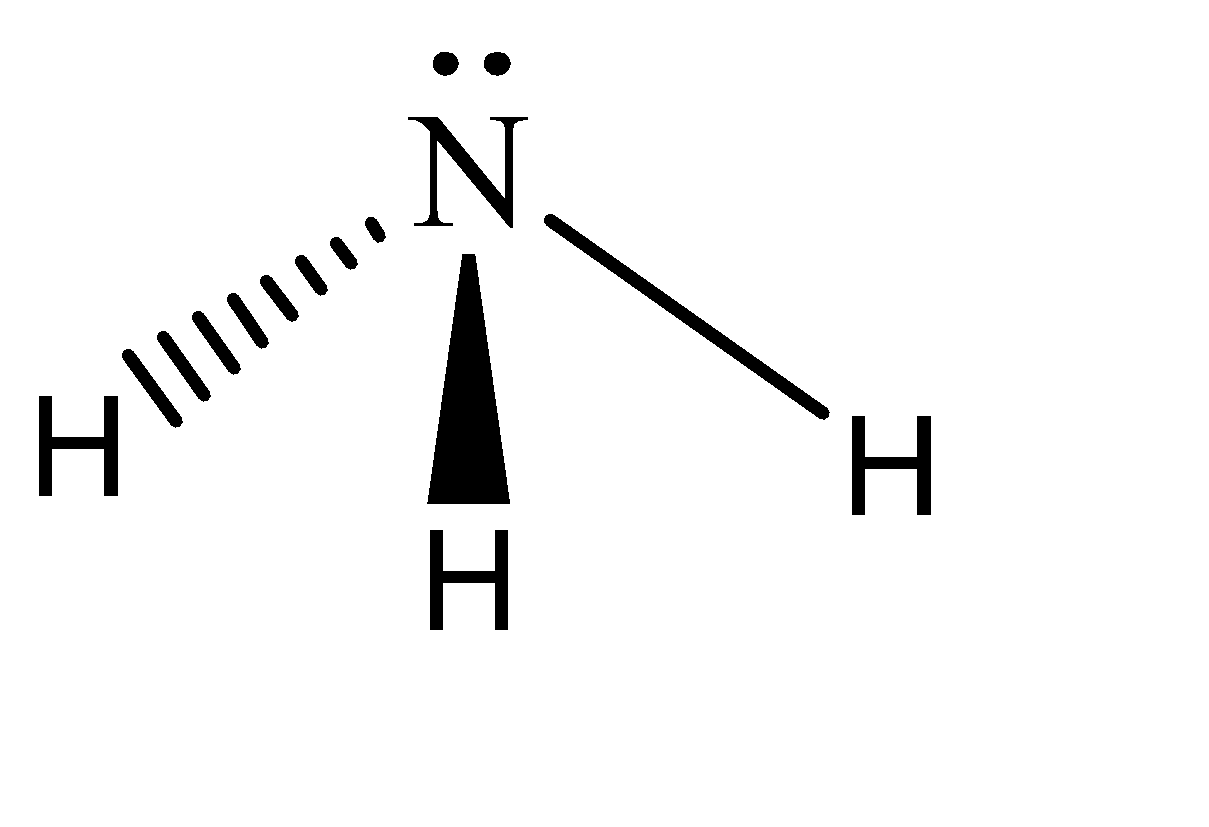
Note:
Another reason hybridisation is necessary is that all the three hydrogens that need to bond to nitrogen have to be identical. Three p orbitals although they appear identical, they aren’t identical, because they face in different directions. To make them behave the same, we’ll have to mix them together and split out an $ s{p^3} $ to bond identically in all three directions.