Question

What does a high and a low z-score mean?

Answer 1

Hint: To do this question first we should know what low and high z-score mean. A high z-score means a very low probability of data above this z-score and a low z-score means a very low probability of data below this z-score.

Complete answer:
A high z-score means a very low probability of data above the z-score. For example, the figure below shows the probability of a z-score above $2.6$.

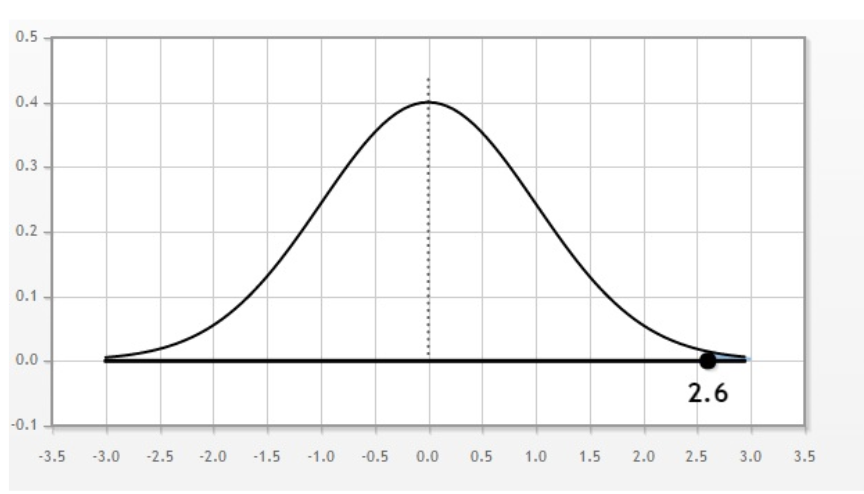
Probability for this is $0.47\% $, which is less than half-percent. Note that if z-score rises further, area under the curve falls and probability reduces further.
A low z-score means a very low probability of data below this z-score. The figure below shows the probability of a z-score below $ - 2.5$.

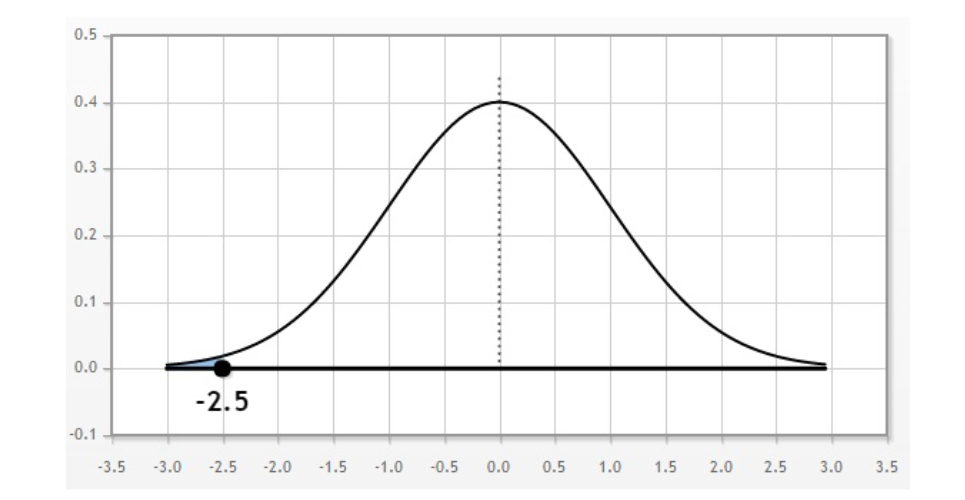
Probability for this is $0.62\% $ and note that if z-score falls further, area under the curve falls and probability reduces further.

Note: Z-score can be defined as the number of standard deviations from the mean. A data point is a measure of how many standard deviations below or above mean. A raw score as a Z-score can also be called as a standard score and it can be placed on a normal distribution curve. Z-scores range from $ - 3$ standard deviations up to $ + 3$ standards. A Z-score can help us in determining the difference or the distance between a value and the mean value. When you "standardize" a variable, its mean becomes zero and its standard deviation becomes one.