
What does a dot product equal to one mean?
Answer
494.7k+ views
Hint: We need to have a basic idea of what a dot product actually means. There are many definitions of dot products. We use the basic definition which states dot product or scalar product is given by: \[\left| A \right| \cdot \left| B \right| = \left| A \right| \cdot \left| B \right|\cos \theta \] where \[\theta \] is the angle between two given vectors.
Complete step by step solution:
The dot product is also called a scalar product. This states that multiplying any two vectors will give us a single vector which is scalar. Here we have considered the vectors as A and B
Scalar product or dot product is basically defined as a product of 2 vectors along with the angle of cosine between them. Look at the formula above , we have written 2 terms \[\left| A \right|and\left| B \right|\], these are called magnitudes of vectors(it is the length of the vector).
According to the question they have given that the dot product is 1. It means that \[A \cdot B = 1\]
Or, \[\left| A \right| \cdot \left| B \right|\cos \theta = 1\]
This is possible only when : \[\cos \theta = 0\],
And \[\cos \theta = 0\] , means that the angle between the 2 vectors A and B is zero.
Hence the 2 vectors are parallel. To get better idea look at the image shown below:
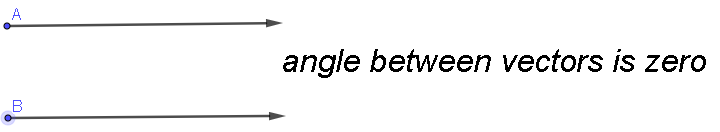
Now the fact that the angle between 2 vectors is 0 means that the vector could be parallel or antiparallel as shown in the image below;

Hence if the dot product is 1 it means that the two given vectors are parallel. And if the dot product is -1 it means that the two given vectors are antiparallel.
Additional Information:
\[ \bullet \] If the angle between 2 given vectors is \[{90^ \circ }\]it means that \[A \cdot B = 0\] and they are said to be orthogonal.
\[ \bullet \] he dot product of a unit vector with itself is given by: \[i \cdot i = j \cdot j = k \cdot k = 1\]
Note:
We should remember that the angle being 0 doesn’t mean that the vectors are only parallel; they can also be antiparallel. Thus when the dot product is 1 it means the vectors are parallel and when the dot product is-1 it means the vectors are anti-parallel.
Complete step by step solution:
The dot product is also called a scalar product. This states that multiplying any two vectors will give us a single vector which is scalar. Here we have considered the vectors as A and B
Scalar product or dot product is basically defined as a product of 2 vectors along with the angle of cosine between them. Look at the formula above , we have written 2 terms \[\left| A \right|and\left| B \right|\], these are called magnitudes of vectors(it is the length of the vector).
According to the question they have given that the dot product is 1. It means that \[A \cdot B = 1\]
Or, \[\left| A \right| \cdot \left| B \right|\cos \theta = 1\]
This is possible only when : \[\cos \theta = 0\],
And \[\cos \theta = 0\] , means that the angle between the 2 vectors A and B is zero.
Hence the 2 vectors are parallel. To get better idea look at the image shown below:
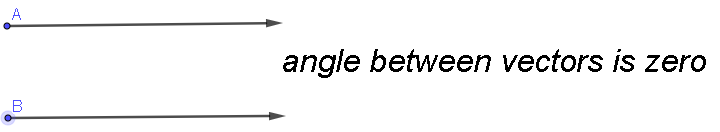
Now the fact that the angle between 2 vectors is 0 means that the vector could be parallel or antiparallel as shown in the image below;

Hence if the dot product is 1 it means that the two given vectors are parallel. And if the dot product is -1 it means that the two given vectors are antiparallel.
Additional Information:
\[ \bullet \] If the angle between 2 given vectors is \[{90^ \circ }\]it means that \[A \cdot B = 0\] and they are said to be orthogonal.
\[ \bullet \] he dot product of a unit vector with itself is given by: \[i \cdot i = j \cdot j = k \cdot k = 1\]
Note:
We should remember that the angle being 0 doesn’t mean that the vectors are only parallel; they can also be antiparallel. Thus when the dot product is 1 it means the vectors are parallel and when the dot product is-1 it means the vectors are anti-parallel.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




