Question

Divide a given line segment in ratio of \[3:5\] and write steps of construction.

Answer 1

Hint: Here, we will draw the given line segment and draw a line having an acute angle with the line segment. We will construct points (which are equal to the sum of the given ratio) at equal distance from each other. We will then join the last point with the end of the line segment and the third point parallel to that line. This will divide the line segment in the required \[3:5\] ratio.

Complete step-by-step answer:
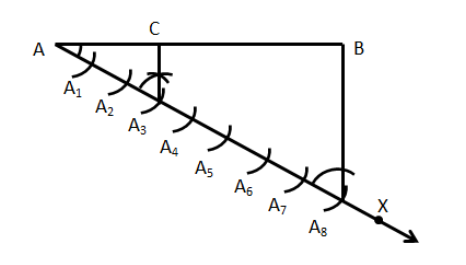
Let \[AB\] be the given line segment.
Now, according to the question, we are required to divide this line segment in the ratio of \[3:5\].
We will follow the steps of construction:
We will draw a line segment \[\overline {AB} \]
Then we will draw a line \[\overrightarrow {AX} \] making an acute angle \[\angle XAB\] with the line segment \[\overline {AB} \].
Now, the given ratio is \[3:5\], hence, we will locate \[\left( {3 + 5} \right) = 8\] points on the line \[\overrightarrow {AX} \]
Let these points be \[{A_1},{A_2},{A_3},{A_4},{A_5},{A_6},{A_7},{A_8}\] such that the distance \[A{A_1} = {A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_7} = {A_7}{A_8}\]
Now, we will join \[B{A_8}\]
Through the point \[{A_3}\], we will draw a vertical line such that it is parallel to the line \[B{A_8}\]
We will make this line by making an angle equal to \[\angle A{A_8}B\] at the point \[{A_3}\]intersecting the line segment \[\overline {AB} \] at point \[C\]
Hence, we have divided the line segment \[\overline {AB} \] such that, \[AC:CB = 3:5\].

Note: Line segment is a part of line that is bounded by two distinct endpoints. In a line segment, the endpoints are known whereas a line does not have any endpoints as it extends endlessly towards infinity in both directions. We should not get confused between a line segment and a ray. A ray has only one endpoint and the other extends to infinity. There are infinite numbers of points in a plane and we can draw an infinite number of line segments using the points.