Question

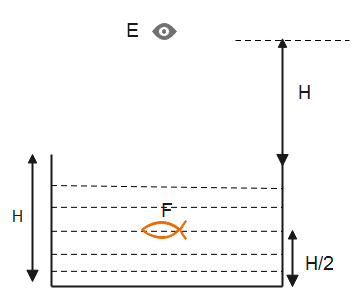
What is the distance of fish F seen by human eyes E
(A). $H+\dfrac{H}{2\mu }$
(B). $\dfrac{H}{\mu }=\dfrac{H}{2}$
(C). $\dfrac{3H}{2\mu }$
(D). None of these

Answer 1

Hint: The observer and the object are in different mediums. Therefore, the observer can see the object at a different height than its original height. The refractive index is a measure of the density of a medium relative to air in terms of speed of light. The ratio of real height to apparent height of the object is the refractive index of the medium.

Formula used:
$\mu =\dfrac{h}{h'}$

Complete step-by-step answer:

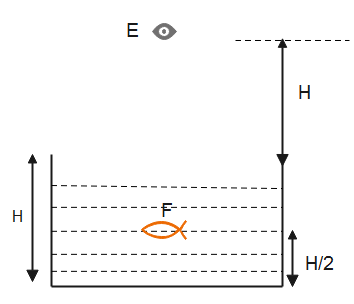
In the given figure, the observer is in the rarer medium and it is observing the fish in denser medium. Therefore, the light travels from rarer medium to denser medium.
The refractive index of a medium is the ratio of the speed of light in the air to the speed of light in medium.
When the object is in the denser medium, the refractive index is given by-
$\mu =\dfrac{h}{h'}$ - (1)
Here, $\mu $ is the refractive index
$h'$ is the apparent height
$h$ is the real height
The real height of the fish is the distance from the eye, from the figure the real height is-
$\begin{align}
  & h=H+\dfrac{H}{2} \\
 & \Rightarrow h=\dfrac{3H}{2} \\
\end{align}$
Therefore, the real height of the fish is $\dfrac{3H}{2}$.
Substituting the value of real height in eq (1), we get,
$\begin{align}
  & \mu =\dfrac{h'}{h} \\
 & \Rightarrow \mu =\dfrac{\dfrac{3H}{2}}{h'} \\
 & \Rightarrow h'=\dfrac{3H}{2\mu } \\
\end{align}$
The depth of the fish as seen from the eyes is $\dfrac{3H}{2\mu }$.
Therefore, the distance of the fish as seen from the eyes is $\dfrac{3H}{2\mu }$.
So, the correct answer is “Option A”.

Note: Refractive index is a constant quantity and is different for different mediums. The denser the medium, the more is the refractive index. When we observe an object in a different medium it appears to be at a different position than its original position, this position is known as apparent height.