Question

Distance between the centres of two stars is $10a$. The masses of these stars are M and 16M and their radii $a$ and \[2a\] respectively. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and $a$.

Answer 1

Hint: Minimum velocity is that velocity where the object just enters the point, where the effective gravitational force is zero. So that smaller star can easily pull it.

Formula Used:

Gravitational Force (F):
$F=\dfrac{GMm}{{{r}^{2}}}$

Kinetic Energy (K):
$K=\dfrac{1}{2}m{{v}^{2}}$

Gravitational Potential Energy (U):
$U=-\dfrac{GMm}{r}$

where:
G= Gravitational constant ($6.67\times {{10}^{-11}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$)
M=Mass of the planet
m= mass of the object
r= distance between the object and planet
v= in this case minimum velocity

Complete step by step answer:
Assuming the object m at that position where effective gravitational force is zero (We are doing this because we want to know what will happen when the object reaches at point O).

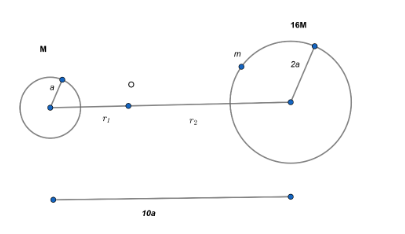
Therefore distance $10a$ is divided into two distances ${{r}_{1}}$ and ${{r}_{2}}$.

Force on particle m due to smaller star (M) = $\dfrac{GMm}{{{r}_{1}}^{2}}$

Force on particle m due to larger star (16M) = $\dfrac{G(16M)m}{{{r}_{2}}^{2}}$

At point O these forces will balance each other, therefore:

\[\dfrac{GMm}{{{r}_{1}}^{2}}=\dfrac{G\left( 16M \right)m}{{{r}_{2}}^{2}}\]

$\begin{align}
  & \Rightarrow {{\left( \dfrac{{{r}_{^{2}}}}{{{r}_{1}}} \right)}^{2}}=16 \\
 & \Rightarrow {{r}_{2}}=4{{r}_{1}} \\
\end{align}$

Also,

$\begin{align}
  & \Rightarrow {{r}_{1}}+{{r}_{2}}=10a \\
 & \Rightarrow {{r}_{1}}+4{{r}_{1}}=10a \\
 & \Rightarrow 5{{r}_{1}}=10a \\
 & \Rightarrow {{r}_{1}}=2a \\
\end{align}$

$\begin{align}
  & \Rightarrow {{r}_{2}}=10a-{{r}_{1}} \\
 & \Rightarrow {{r}_{2}}=10a-2a \\
 & \Rightarrow {{r}_{2}}=8a \\
\end{align}$

In question we have to launch an object from a larger star (16M) to place that object at O, so that it can be pulled by a smaller star (M).

Therefore, by applying Energy conservation Law.

Energy conservation law: Energy is always conserved or we can say total initial energy equals to total final energy.

Mathematically,

$K{{E}_{surface}}+P{{E}_{surface}}=K{{E}_{O}}+P{{E}_{O}}$
Where, KE=kinetic energy and PE= potential energy

$\begin{align}
& \dfrac{1}{2}m{{v}^{2}}_{\min }+\left( -\dfrac{16GMm}{2a}-\dfrac{GMm}{10a-2a} \right)=0-\dfrac{16GMm}{8a}-\dfrac{GMm}{2a} \\
&\Rightarrow \dfrac{1}{2}m{{v}^{2}}_{\min }=\dfrac{16GMm}{2a}+\dfrac{GMm}{8a}-\dfrac{16GMm}{8a}-\dfrac{GMm}{2a} \\
 & \Rightarrow \dfrac{1}{2}m{{v}^{2}}_{\min }=\dfrac{GMm}{a}\left( 8+\dfrac{1}{8}-2-\dfrac{1}{2} \right) \\
 & \Rightarrow \dfrac{1}{2}m{{v}^{2}}_{\min }=\dfrac{45}{8}\dfrac{GMm}{a} \\
 & \Rightarrow {{v}^{2}}_{\min }=\dfrac{45}{4}\dfrac{GM}{a} \\
 & \Rightarrow {{v}_{\min }}=\sqrt{\dfrac{45}{4}\dfrac{GM}{a}} \\
 & \\
\end{align}$

Note: There are certain things to keep in mind:
1.) At point O the object just stops because the gravitational force by both the stars cancel each other. Therefore, final velocity becomes zero and so final kinetic energy.
2.) Negative sign in gravitational potential energy shows the pull or attraction.