Question

Discuss with theory the method of inducing emf in a coil by changing its orientation with respect to the direction of the magnetic field.

Answer 1

Hint: This problem is related to the Michael Faraday’s famous law of electromagnetic induction which states that “a voltage is induced in a circuit whenever relative motion exists between a conductor and a magnetic field and that the magnitude of this voltage is proportional to the rate of change of the flux”.

Complete answer:
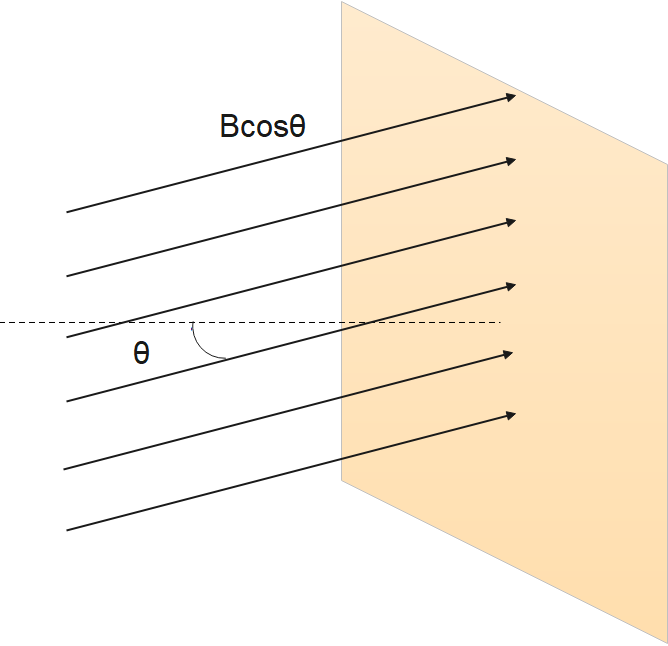
The concept of induced EMF involves generating a voltage by changing the magnetic field that passes through a coil of wire. The magnetic flux is a measure of the number of magnetic field lines passing through an area. If a loop of wire with an area A is in a magnetic field B, the magnetic flux is given by:
$\phi =BA\cos \theta $
where B is the magnetic field strength over an area A, at an angle θ with the perpendicular to the area as shown in Figure below.

If the flux changes, an emf will be induced. There are therefore three ways an emf can be induced in a loop:
a.) Change the magnetic field.
b.) Change the area of the loop.
c.) Change the angle between the field and the loop.
If there are N turns in the coil, magnetic flux will be:
\[\phi =NBA\cos \theta (as\text{ }\theta \text{=}\omega \text{t)}\]
where ω is the angular velocity of the coil. The induced emf (e) is:
$e=-\dfrac{d\phi }{dt}=NBA\dfrac{d}{dt}\cos \omega t$
Hence, $e=NBA\omega \cos \omega t$
To evaluate the value of e for different orientations we need to consider different values of θ.
A.) For \[~\omega t=0\], i.e. the plane of the coil is perpendicular to the field B e = 0.
B.) For \[~\omega t=\dfrac{\pi }{2}\] ,i.e. the plane of the coil is parallel to B $e=NBA\omega $
C.) For \[~\omega t=\pi \], i.e. the plane of the coil is at right angle to B e = ​0.
D.) For\[~\omega t=\dfrac{3\pi }{2}\] , i.e. the plane of the coil is again parallel to B $e=-NBA\omega $
E.) For\[~\omega t=2\pi \], i.e. the plane of the coil is perpendicular to the field B e = 0.

Note:
Units of magnetic flux $\phi $ are $T{{m}^{2}}$. As seen in Figure,$B\cos \theta ={{B}_{\bot }}$, which is the component of B perpendicular to the area A. Thus magnetic flux is $\phi ={{B}_{\bot }}A$, the product of the area and the component of the magnetic field perpendicular to it.