Question

What is the directrix in the conic section?

Answer 1

Hint: We first explain the conic sections and the use for the directrix in making the conic sections. We take the general equations and find their directrix.

Complete step by step solution:
A conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic sections are the hyperbola, the parabola, and the ellipse. The circle is a type of ellipse, and is sometimes considered to be a fourth type of conic section.
While each type of conic section looks very different, they have some features in common. For example, each type has at least one focus and directrix. A directrix is a line used to construct and define a conic section. The distance of a directrix from a point on the conic section has a constant ratio to the distance from that point to the focus. As with the focus, a parabola has one directrix, while ellipses and hyperbolas have two.
As example the directrix for the conic sections like parabola with general formula ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$ will be $y+a=\beta $ and for ellipse with general formula \[\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1\] will be $x=\alpha \pm \dfrac{a}{e}$.

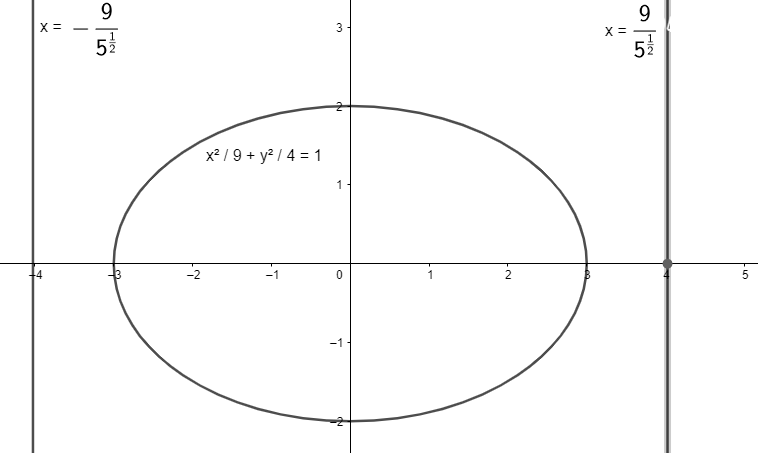
Note: The directrix of a conic section represents the line which together with focus defines the conic section where distance from the focus is proportional to the horizontal distance from the directrix.