Question

What is diffraction of light? Obtain condition for the bright and dark fringes in diffraction pattern due to a single narrow slit illuminated by a monochromatic source of light.

Answer 1

Hint: When attempting questions based on diffraction, keep in mind the concepts regarding diffraction like what causes it , what are the various conditions required for it to happen, what are the phenomena that happen when light travels in air and when it comes in contact with obstacles.

Complete step by step solution:
When light travels in air, it encounters various phenomena like interference, refraction, reflection and diffraction. When the light comes in contact with an obstacle, diffraction of light takes place. When light passes through a small opening, comparable in size to the wavelength \[\lambda \] of the light, the wave front on the other side of the opening resembles the wave.
When monochromatic light is made on a single slit, we get a diffraction pattern on a screen placed behind the slit. The diffraction pattern contains bright and dark bands , also called bright and dark fringes, and the intensity of the central band is maximum and goes on decreasing on both sides.
In the single-slit diffraction experiment, we can observe the bending phenomenon of light or diffraction that causes light from a coherent source to interfere with itself and produce a distinctive pattern on the screen called the diffraction pattern. Diffraction is evident when the sources are small enough that they are relatively the size of the wavelength of light. For large slits, the spreading out is small and generally unnoticeable.
For easier calculation let us assume the slit width \[a\] << \[D\] where \[D\] is the separation between slit and source.

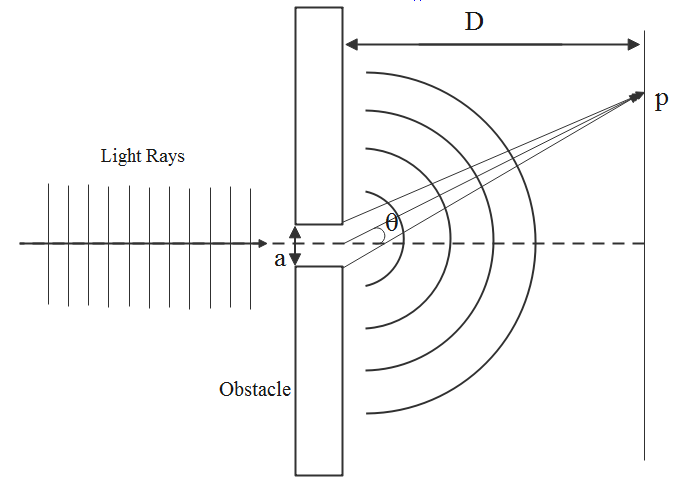
Identify the angular position of any point on the screen by \[\theta \] measured from the slit centre which divides the slit by \[\dfrac{a}{2}\] lengths. To describe the pattern in an easier way, first see the conditions required for dark fringes. Divide the split into zones of equal widths of \[\dfrac{a}{2}\] and consider a pair of rays that emanate from distances \[\dfrac{a}{2}\] from each other.
Keep in mind this calculation will only be valid if \[D\] is very large.
Consider any number of ray pairings starting from a distance \[\dfrac{a}{2}\] from one another such as the bottom two rays. Any arbitrary pair of rays at a distance \[\dfrac{a}{2}\] can also be considered.
For a dark fringe, the path difference must cause destructive interference, the path difference must be out of phase by \[\dfrac{\lambda }{2}\] where \[\lambda \] is the wavelength.

Note: Young’s double slit experiment gave definitive proof of the wave character of light. An interference pattern is obtained by the superposition of light from two slits. There is constructive interference and destructive interference occurring in the experiment.