Question

Why is it difficult to walk on slippery roads?

Answer 1

Hint: Slippery roads have very low coefficient of friction. First, we will see how the frictional force due to the ground helps us to move. Further, we will analyze how the frictional force is related to the coefficient of friction and accordingly determine why exactly it is difficult to walk on slippery surfaces.
Formula used:
${{F}_{FRIC}}=\mu N$

Complete step-by-step solution:
When we walk on the ground we basically push the ground backward at a particular angle. Let us say the force with which we press the ground is F. A brief vector diagram of this scenario is shown in the figure below.

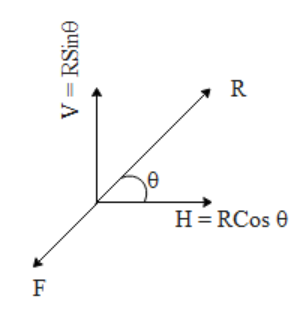
In the above diagram we see that as a consequence of force F, the ground exerts an equal and opposite reaction force R. Let us say the reaction force makes an angle $\theta $ with the ground. Therefore the vertical component of R i.e. V is equal to $V=RSin\theta $ and horizontal component i.e. H is equal to $H=RCos\theta $.
If the surface is very smooth i.e. slippery, the force due to friction due to the ground on the feet will be very small. If $\mu $ is the coefficient of friction of the slippery surface the force of friction is given by ${{F}_{FRIC}}=\mu N$ where N is the normal due to the surface. In the above case, it is equal to $V=RSin\theta $> The amount of force (F)applied on the ground is proportional to the frictional force. If the surface is slippery the feet will slip back as the coefficient of friction will be very small. As a consequence, the reaction force will be very small. Therefore we can conclude that the horizontal component of the reaction force which helps us to move forward will also be very small.
It is because of this we find it very difficult to walk on slippery surfaces.

Note: The vertical component of the reaction force keeps us stable while walking. Whereas the horizontal component keeps us moving forward. It is to be noted that one always has to take small steps while walking on slippery surfaces as the legs will almost remain vertical and will be able to move steadily.