Question

What is the difference between the graph of \[y = \left| {f\left( x \right)} \right|\] and \[\left| y \right| = f\left( x \right)\].

Answer 1

Hint: Here we will first assume the function \[f\left( x \right)\]. Then we will form the equations by putting the value of the function \[f\left( x \right)\]. We will then plot the graph on the basis of the equation and will compare the graph of the both given equations.

Complete step-by-step answer:
Given functions are
\[y = \left| {f\left( x \right)} \right|\]…………………..\[\left( 1 \right)\]
\[\left| y \right| = f\left( x \right)\]…………………..\[\left( 2 \right)\]
Let the function \[f\left( x \right)\] be equal to \[f\left( x \right) = x\].
Now we will form the graph for the respective equations.
For equation \[\left( 1 \right)\], the equation becomes
\[ \Rightarrow y = \left| x \right|\]
So from the equation it is clearly seen that the graph for the equation \[\left( 1 \right)\] will be symmetric to the Y-axis of the graph because for every value of \[x\] the value of \[y\] will always remain positive. Therefore, the graph is

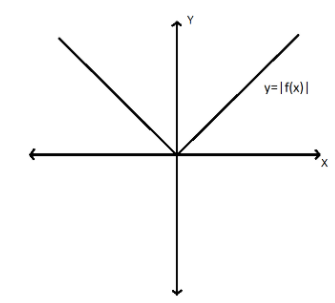
Now we will take the equation \[\left( 2 \right)\]. Therefore, the equation becomes
\[ \Rightarrow \left| y \right| = x\]
So from the equation it is clearly seen that the graph for the equation \[\left( 2 \right)\] will be symmetric to the X-axis of the graph because for every value of \[y\] the value of \[x\] will always remain positive. Therefore, the graph is

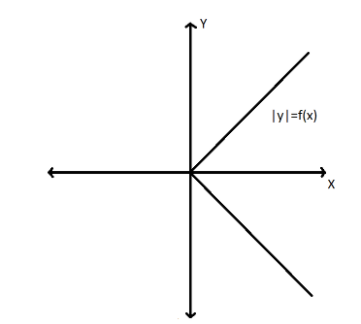
Hence the graph for equation \[\left( 1 \right)\] will be symmetric about the Y-axis and the graph for the equation \[\left( 2 \right)\] will be symmetric about the X-axis.

Note: The given functions are modulus functions. Modulus function is the function which always gives the positive value for the given input whether the given input is positive or negative.
For example: \[\left| a \right| = a\] and \[\left| { - a} \right| = a\].
To draw the graph we need to note a few points. The \[x\] axis and \[y\] axis in the Cartesian plane are perpendicular to each other and intersecting at a point which is named as the origin. The positive \[x\] axis is towards the right side of the origin and negative \[x\]-axis is towards the left side of the origin. Also the positive \[y\] axis lies towards the upward direction from the origin and the negative \[y\] axis lies towards the downward direction from the origin.