Question

What is the difference between medians, perpendiculars bisectors, and altitudes?

Answer 1

Hint: With reference to a triangle, the term median, perpendicular bisector and altitude seems very similar however they are different terms with different purpose. They all go to an opposite vertex. Both median and altitude start from one of the three vertices. Their differences are that the perpendicular bisector must be ninety degrees, or it'll be a median. The perpendicular line taken from the triangle's vertex to the opposite side is called the altitude.

Complete step-by-step answer:
Let us understand the difference between them:
Median: A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid.
Let us understand with the help of a diagram as follows:

In the given figure of \[\vartriangle ABC\] , the three medians are \[\overline {AA'} \] , \[\overline {BB'} \] and \[\overline {CC'} \] . Point \[T\] is the centroid.

Perpendicular Bisector: Perpendicular line or segment is a perpendicular line that passes through the midpoint for the side of the triangle is called perpendicular bisector.

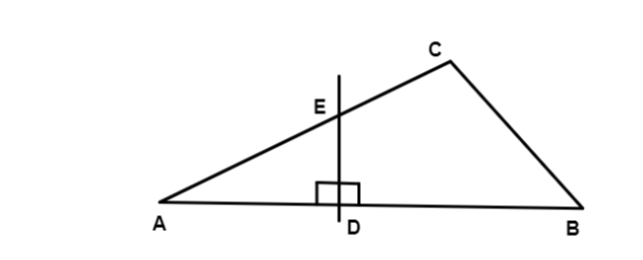
In above \[\vartriangle ABC\] , \[D\] is the midpoint of \[\overline {AB} \] and \[\overline {ED} \] is the perpendicular bisector.

Altitude: It is a line that extends from one vertex of a triangle perpendicular to the opposite side which is the base of the triangle. It is also known as the height of the triangle.

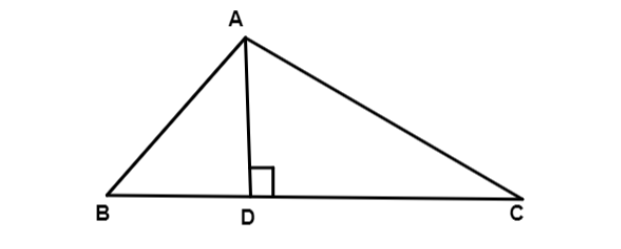
In above \[\vartriangle ABC\] , \[\overline {AD} \] is the altitude from vertex \[A\] perpendicular to \[\overline {BC} \] .

Note: In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length.
Use scale, rounder and compass to draw the medians, bisectors and altitude.
Every perpendicular bisector is a median but not every median is a perpendicular bisector.
Altitude may or may not be a perpendicular bisector of a triangle.