Question

What is the difference between Medians, Perpendicular Bisectors and Altitudes?

Answer 1

Hint: To know the difference between medians, perpendicular Bisectors and Altitudes, we should be aware of definitions of all three mentioned above. Also know the midpoint, line segment, vertex and also about angles.

Complete step-by-step answer:
Median: Consider the triangle \[\vartriangle ABC\].\[\overline {BD} \] is a median, median is a line segment that extends from vertex from one side of triangle B to midpoint D of line segment \[\overline {AC} \]. Midpoint breaks the line segments A and C as shown below

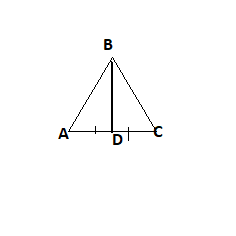
\[\therefore \]\[\overline {AD} \]\[ \cong \]\[\overline {CD} \]
Altitudes:
\[\overline {BD} \] is an altitude which is line segment but different from median but it does not splits.
It simply forms right angles.

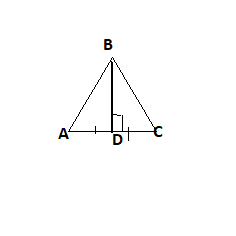
the line segment is perpendicular
\[\therefore \]\[\overline {BD} \]\[ \bot \] \[\overline {AC} \] it forms right angles
\[\therefore \]\[\angle ABC\]\[ \cong \]\[\angle CDB\]=\[{90^o}\]
Altitude simply connects the vertex of one side of triangle to half the segment.
Perpendicular Bisectors:
Consider AB, the line passes through AB. Let us say \['l'\]passes through line AB called as perpendicular bisector of AB that is line \['l'\] is \[ \bot \]bisector of \[\overline {AB} \]. perpendicular bisector is basically combination of median and Altitude.

   

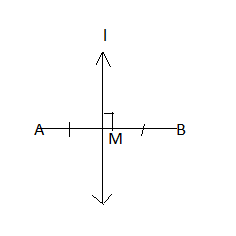
Like Altitude, it forms right angle and like median it splits segment into two parts which are congruent.
M is the midpoint and \[\overline {AM} \]is \[ \cong \]\[\overline {BM} \] so perpendicular bisector as features of altitude and median.

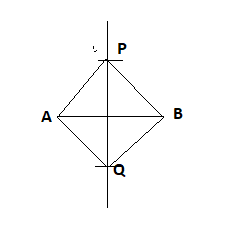
P is equal to equidistant point to endpoints of the segments.
\[\therefore \]AP and PB are congruent and AQ and QB are congruent.

Note: Definitions
Median: A Median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.
Every triangle has exactly three medians.
Altitude: An altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base.
Vertex: Vertex is formed when two lines or line segments or rays intersect.