
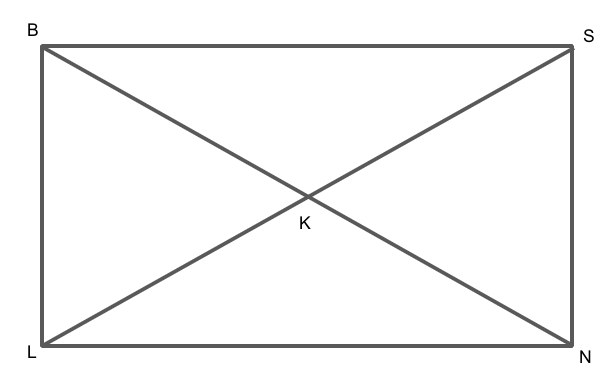
Diagonals LS and BN of rectangle BSNL intersect each other at point K. If \[{\text{KL}} = 7{\text{ cm}}\], find LS and BN. (see figure)

Answer
587.1k+ views
Hint: First we will use that in parallelogram BSNL, the sides BS and LN are equal and \[{\text{BS||LN}}\] by our given diagram. In triangles \[\Delta {\text{LKN}}\] and \[\Delta {\text{SBK}}\], if \[{\text{BS||LN}}\] and BN is the transversal \[\angle LNK\] and \[\angle SBK\] being the alternate angles are equal and SL is the transversal \[\angle KLN\] and \[\angle KSB\] being the alternate angles are equal. As the line segment BS is equal to LN, we have \[{\text{BS}} = {\text{LN}}\]. Then use ASA rule, to prove the angles to be congruent. Then use the corresponding parts of congruent triangles to prove the line segments KL and SK are equal.
Then use \[LS = 2KL\] to find the value of LS and then rectangle property to find the value of BN.
Complete step by step answer:
We are given that the diagonals LS and BN of rectangle BSNL intersect each other at point K.
We know that in parallelogram BSNL, the sides BS and LN are equal and \[{\text{BS||LN}}\] by our above construction.
Consider triangles \[\Delta {\text{LKN}}\] and \[\Delta {\text{SBK}}\],
We know that if \[{\text{BS||LN}}\] and BN is the transversal \[\angle LNK\] and \[\angle SBK\] being the alternate angles, we have
\[ \Rightarrow \angle LNK = \angle SBK\]
We also know that if \[{\text{BS||LN}}\] and SL is the transversal \[\angle KLN\] and \[\angle KSB\] being the alternate angles, we have
\[ \Rightarrow \angle KLN = \angle KSB\]
As the line segment BS is equal to LN, we have \[{\text{BS}} = {\text{LN}}\].
We know that in AAS rule, when two angles and a side of two triangles are same, then the both triangles are congruent with each other.
Using the above AAS rule, we get
\[\therefore \Delta {\text{LKN}} \cong \Delta {\text{SKB}}\]
Being the corresponding parts of congruent triangles \[\Delta {\text{LKN}}\] and \[\Delta {\text{SKB}}\], the line segments KL and SK are equal.
We are given that KL is 7 cm.
This implies that \[LS = 2KL\].
Substituting the given value of KL in the above equation, we get
\[
\Rightarrow LS = 2 \times 7 \\
\Rightarrow LS = 14{\text{ cm}} \\
\]
We know that in a rectangle both the diagonals are equal, so BN is equal to LS.
\[ \Rightarrow BN = 14{\text{ cm}}\]
Note: In solving these types of questions, you need to know that the properties of rectangles and their diagonals. Then we will use the properties accordingly. This is a simple problem, one should only need to know the definitions. It is clear from the diagram that it is a rectangle as nowhere it is given it to be a square, so remember that as well.
Then use \[LS = 2KL\] to find the value of LS and then rectangle property to find the value of BN.
Complete step by step answer:
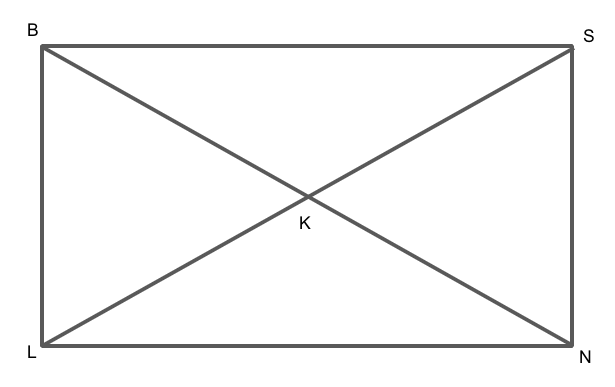
We are given that the diagonals LS and BN of rectangle BSNL intersect each other at point K.

We know that in parallelogram BSNL, the sides BS and LN are equal and \[{\text{BS||LN}}\] by our above construction.
Consider triangles \[\Delta {\text{LKN}}\] and \[\Delta {\text{SBK}}\],
We know that if \[{\text{BS||LN}}\] and BN is the transversal \[\angle LNK\] and \[\angle SBK\] being the alternate angles, we have
\[ \Rightarrow \angle LNK = \angle SBK\]
We also know that if \[{\text{BS||LN}}\] and SL is the transversal \[\angle KLN\] and \[\angle KSB\] being the alternate angles, we have
\[ \Rightarrow \angle KLN = \angle KSB\]
As the line segment BS is equal to LN, we have \[{\text{BS}} = {\text{LN}}\].
We know that in AAS rule, when two angles and a side of two triangles are same, then the both triangles are congruent with each other.
Using the above AAS rule, we get
\[\therefore \Delta {\text{LKN}} \cong \Delta {\text{SKB}}\]
Being the corresponding parts of congruent triangles \[\Delta {\text{LKN}}\] and \[\Delta {\text{SKB}}\], the line segments KL and SK are equal.
We are given that KL is 7 cm.
This implies that \[LS = 2KL\].
Substituting the given value of KL in the above equation, we get
\[
\Rightarrow LS = 2 \times 7 \\
\Rightarrow LS = 14{\text{ cm}} \\
\]
We know that in a rectangle both the diagonals are equal, so BN is equal to LS.
\[ \Rightarrow BN = 14{\text{ cm}}\]
Note: In solving these types of questions, you need to know that the properties of rectangles and their diagonals. Then we will use the properties accordingly. This is a simple problem, one should only need to know the definitions. It is clear from the diagram that it is a rectangle as nowhere it is given it to be a square, so remember that as well.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




