Question

How many diagonals are there in a hexagon?
$
  A.{\text{ 6}} \\
  B.{\text{ 4}} \\
  {\text{C}}{\text{. 11}} \\
  {\text{D}}{\text{. 9}} \\
 $

Answer 1

Hint: Here in this question we go through the properties of polygon. We know many types of polygon. For this question we should have to use the properties of the hexagon to find the number of diagonals.
The formula for finding the number of diagonal from n sided polygon I.e. $\left[ {\dfrac{{n(n - 1)}}{2} - n} \right]$

Complete step-by-step answer:
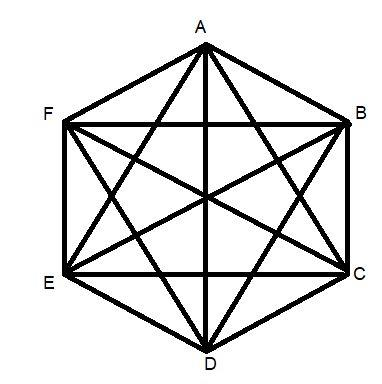
We have to find out the number of diagonals in a hexagon . For this we made the diagram of hexagon recoiling the definition of hexagon.
A hexagon is a polygon with 6 sides and 6 angles. When we join the vertices which are not adjacent we will find the number of diagonals in the hexagon. All the sides of a hexagon meet with each other end to end to form a shape.
By the help of diagrams we can also name the diagonals.
The diagonals are AE, AD, AC, BD, BE, BF, CE, CF and DF.
By counting we can say that, the number of diagonals in hexagon = 9.
So option D is the correct answer.

SECOND METHOD
We know that the formula for finding the number of diagonal from n sided polygon I.e. $\left[ {\dfrac{{n(n - 1)}}{2} - n} \right]$
And here it is a hexagon therefore the value of n is 6.
Now put the value of n in the formula we get,
$
   = \left[ {\dfrac{{6(6 - 1)}}{2} - 6} \right] \\
   = \dfrac{{6 \times 5}}{2} - 6 \\
   = 9 \\
 $
Hence option D is the correct answer.

Note: Whenever we face such a question. We have to go through the definition of that figure. And draw the diagram of that figure by the definition and then count the number of diagonals. You will also find the number of diagonals by applying the formula.