Question

Diagonal of a quadrilateral JOSH intersect at P in such a way that ar(JHP) =ar(OPH). Prove that JOSH is a trapezium.

Answer 1

Hint: You are given a quadrilateral JOSH whose diagonal intersect each other at some point P and after the intersection of the two diagonals you will get triangles and the opposite triangle $\Delta JPH$ and $\Delta OPS$ has same area. You need to prove that JOSH is a trapezium. For clear understanding look at the diagram drawn below
Diagram-

Complete step-by-step answer:
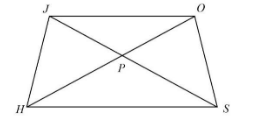
Given: The diagonals of a quadrilateral intersect each other at a point P. You can see in the diagram $\overline {JS} $ and $\overline {OH} $ are intersecting each other and area of $\Delta JPH$ is equal to area of $area{\text{ }}of\Delta JPH = area{\text{ }}of\Delta OPS$
To prove JOSH is a trapezium
Proof:
We know that a trapezium is a quadrilateral that has one pair (that means two) of opposite sides which are parallel to each other.
So, we need to show two sides of JOSH parallel to each other and we can prove that JOSH is trapezium.
We are given,
$area{\text{ }}of\Delta JPH = area{\text{ }}of\Delta OPS$
Now, let us add the area of the triangle $\Delta PHS$ on both the sides,

$area{\text{ }}of\;\Delta JPH + {\text{ }}area{\text{ }}of\Delta PHS\; = area{\text{ }}of\;\Delta OPS + {\text{ }}area{\text{ }}of\Delta PHS \\
\Rightarrow ar\left( {\Delta JPH} \right) + ar\left( {\Delta PHS} \right) = ar\left( {\Delta OPS} \right) + ar\left( {\Delta PHS} \right)$ \\

Look at the diagram, you can see that area of \[\Delta JHS\] and area of $\Delta PHS$ given us the area of \[\Delta JHS\]
Similarly, area of $\Delta OPS$ and area of $\Delta PHS$ given us the area of \[\Delta OSH\]
So,

 $ar\left( {\Delta JPH} \right) + ar\left( {\Delta PHS} \right) = ar\left( {\Delta OPS} \right) + ar\left( {\Delta PHS} \right) \\
 \Rightarrow ar\left( {\Delta JHS} \right) = ar\left( {\Delta OSH} \right)$ \\

Which implies the area of the triangle \[\Delta JHS\] and area of \[\Delta OSH\] triangle are equal.
We know that,
Two triangles having the same base and equal area lie between the parallel lines.
Which means, since \[\Delta JHS\] and \[\Delta OSH\] have the same area and also same base \[\overline {SH} \], then the line \[\overline {SH} \] and \[\overline {JO} \], between which \[\Delta JHS\] and \[\Delta OSH\] lie are parallel to each other.
i.e. \[\overline {SH} \parallel \overline {JO} \]
We know,
If a quadrilateral has two lines which are opposite and parallel to each other it is called a trapezium.
So, JOSH is a trapezium.

Note: You should know all the properties of different quadrilaterals to solve equations like this. Students often get confused about what is trapezium or rectangle or rhombus. You should have a good concept to avoid such confusion.