Question

How do you determine whether the graph of $\left| x \right|=-3y$ is symmetric with respect to the $x$ axis, $y$ axis or neither?

Answer 1

Hint: Here in this problem firstly we need to consider the equation and analyze whether the given equation is symmetric to $x$ or $y$ axis, to find this we need to know about the modulus that is given in this problem, modulus only takes the positive values of any value for $x$ here,

Complete step-by-step solution:
If a relationship is symmetric to the $y$ axis then every point $\left( x,y \right)$ defined by that relationship is reflected through the $y$ axis as a point $\left( -x,y \right)$ which is also a member of that relationship.
That is if a relationship is symmetric to the $y$ axis, we can replace all occurrences of $x$ with $\left( -x \right)$ and the relationship will remain the same.
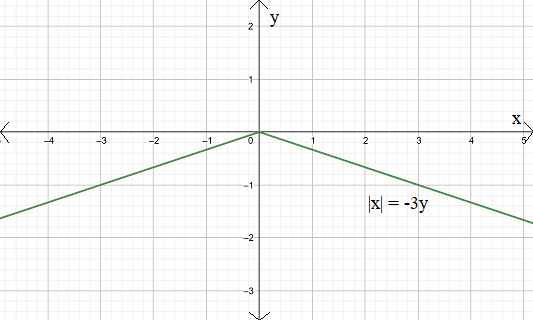
Given the relationship:$\left| x \right|=-3y$
since $\left| x \right|=\left| -x \right|$
$\left| x \right|=-3y$ is identical to $\left| -x \right|=-3y$
and the relationship is symmetric to the $y$ axis and not symmetric along $x$-axis respectively.

Note: In this problem one should be careful of the modulus values and one should know about it, that it takes only positive values in it, or else the whole problem may go wrong, and in other case one should have the knowledge of plotting the graph and should have the knowledge of quadrants that in which quadrant negative values are plotted, without these knowledge one may totally go wrong with this given problem, and student may go wrong in analysing the symmetry of the given problem that whether it is symmetric to $x$ or $y$ axis, one should take care of that problem .