
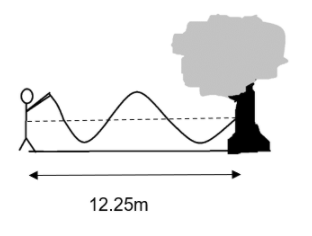
Determine the wavelength of the wave caused by the rope whose one end is attached to a tree and other end is swung by a person as shown below:
A) 8 m
B) 7 m
C) 6 m
D) 5 m

Answer
579.6k+ views
Hint: The wavelength of the rope can be determined by using the total length of the column from the man to the tree. The experiment looks similar to a string attached at one end. We need to see the number of waves involved and thus, calculate the wavelength.
Complete answer:
Let us consider the harmonics involved in a vibration of longitudinal waves. We know that they have strict conditions when the ends are open or closed. In the case of the transverse waves, the node and antinodes are formed with respect to the source.
Let us consider our figure. In order to find the wavelength of the rope wave, we need to find the number of wavelengths that the rope creates with the tree.
On close observation, we can conclude that there is only one complete wave in the figure.
Other than the full wave, there is three-quarters of another wave. So, we can say that the total waves in the rope is \[(1+\dfrac{3}{4})\lambda \]. This can be further equated to the total length of the column between the man and the tree.
i.e.,
\[L=(1+\dfrac{3}{4})\lambda \]
From this equation we can get the wavelength of the rope wave as –
\[\begin{align}
& L=(1+\dfrac{3}{4})\lambda \\
& Given\text{ L =12}\text{.25m} \\
& \Rightarrow \lambda \text{=}\dfrac{4L}{7} \\
& \Rightarrow \lambda \text{=}\dfrac{4\times 12.25}{7} \\
& \Rightarrow \lambda \text{=}7m \\
\end{align}\]
Therefore. The wavelength of the rope wave in the given figure has a wavelength of 7m.
The correct answer is option B.
Additional Information:
The wavelength depends on the number of harmonics between the two ends of the rope.
Note:
For the same rope, we can have a longer wavelength if the number of oscillations is further reduced. The wavelength will be equal to the length if the number of waves is 1. The frequency increases as the number of waves increases and that decreases the wavelength.
Complete answer:
Let us consider the harmonics involved in a vibration of longitudinal waves. We know that they have strict conditions when the ends are open or closed. In the case of the transverse waves, the node and antinodes are formed with respect to the source.
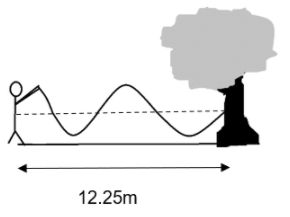
Let us consider our figure. In order to find the wavelength of the rope wave, we need to find the number of wavelengths that the rope creates with the tree.
On close observation, we can conclude that there is only one complete wave in the figure.

Other than the full wave, there is three-quarters of another wave. So, we can say that the total waves in the rope is \[(1+\dfrac{3}{4})\lambda \]. This can be further equated to the total length of the column between the man and the tree.
i.e.,
\[L=(1+\dfrac{3}{4})\lambda \]
From this equation we can get the wavelength of the rope wave as –
\[\begin{align}
& L=(1+\dfrac{3}{4})\lambda \\
& Given\text{ L =12}\text{.25m} \\
& \Rightarrow \lambda \text{=}\dfrac{4L}{7} \\
& \Rightarrow \lambda \text{=}\dfrac{4\times 12.25}{7} \\
& \Rightarrow \lambda \text{=}7m \\
\end{align}\]
Therefore. The wavelength of the rope wave in the given figure has a wavelength of 7m.
The correct answer is option B.
Additional Information:
The wavelength depends on the number of harmonics between the two ends of the rope.
Note:
For the same rope, we can have a longer wavelength if the number of oscillations is further reduced. The wavelength will be equal to the length if the number of waves is 1. The frequency increases as the number of waves increases and that decreases the wavelength.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




