Question

How‌ ‌do‌ ‌you‌ ‌determine‌ ‌the‌ ‌slant‌ ‌asymptotes‌ ‌of‌ ‌a‌ ‌hyperbola?‌ ‌ ‌

Answer 1

Hint: To determine the slant asymptote of a hyperbola firstly we should consider the mathematical form of Hyperbola and then modify it such that we get it as equation equating to y and then the equation is simplified with the assumptions we make. The values obtained are the slant asymptotes of the hyperbola.

Complete step-by-step solution:
Let us find the slant asymptotes of a hyperbola of the form, the mathematical representation of a hyperbola is as below,
 \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
By subtracting \[\dfrac{{{x}^{2}}}{{{a}^{2}}}\] on both LHS and RHS we get,
\[\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}-\dfrac{{{x}^{2}}}{{{a}^{2}}}=1-\dfrac{{{x}^{2}}}{{{a}^{2}}}\]
\[\Rightarrow -\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-\dfrac{{{x}^{2}}}{{{a}^{2}}}\]
Now we are suppose to multiplying by\[-{{b}^{2}}\], to get only terms of y in the LHS,
\[\Rightarrow {{y}^{2}}=\dfrac{{{b}^{2}}}{{{a}^{2}}}{{x}^{2}}-{{b}^{2}}\]
In next step take the square root on both the side of the equation to remove the square from y term present in the LHS,
\[\Rightarrow y=\pm \sqrt{\dfrac{{{b}^{2}}}{{{a}^{2}}}{{x}^{2}}-{{b}^{2}}}\]
Here For large value of x, we can say that \[-{{b}^{2}}\] in the square root is negligible, so we can neglect it from the above equation, so we can write the equation as mentioned below,
\[\Rightarrow y=\pm \sqrt{\dfrac{{{b}^{2}}}{{{a}^{2}}}{{x}^{2}}-{{b}^{2}}}\approx \pm \sqrt{\dfrac{{{b}^{2}}}{{{a}^{2}}}{{x}^{2}}}=\pm \dfrac{b}{a}x\]
Hence, the slant asymptotes of the hyperbola are as follows,
\[y=\pm \dfrac{b}{a}x\].
i.e. \[y=+\dfrac{b}{a}x\] and \[y=-\dfrac{b}{a}x\]

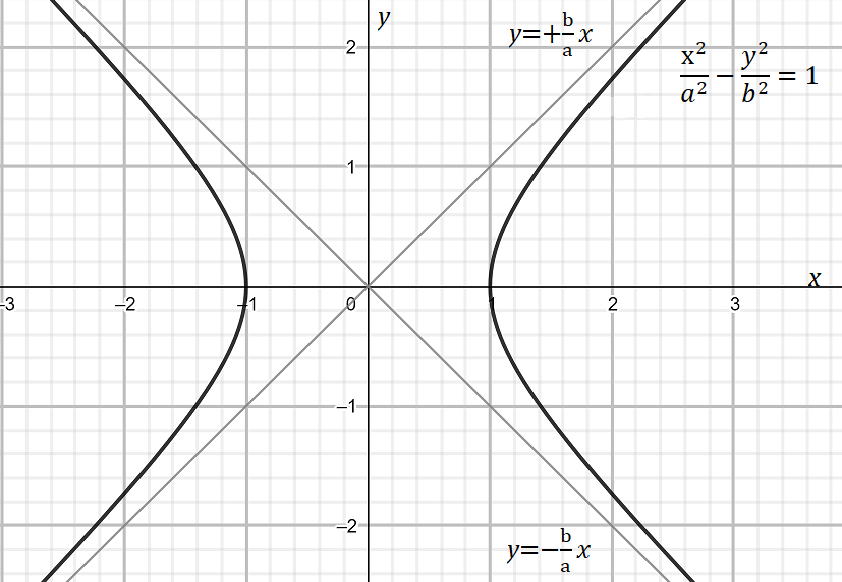
Note: It is required to know the mathematical representation of the hyperbola i.e. \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]. Students usually can go wrong in transforming the equation to make it equated to y to get the slant asymptotes of hyperbola. It is also necessary to make the assumptions such that we can simplify the equation further.