Question

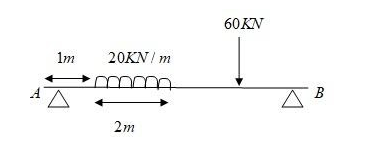
Determine the reaction at support $ A $ and $ B $ of loaded beam shown in figure below.

Answer 1

Hint: As we know that we can use a concept of equilibrium in this question, as given the beam is balancing the load applied in a downward direction with supports on both ends, the supports of the same magnitude but in opposite directions.
Given First downward load, $ {L_1} = 60KN $
Second downward load $ {L_2} = 20KN/m $
Distance where second downward load occur, $ D = 2m $
Now, Second downward load will be, $ 20KN/m \times 2m = 40KN $ .

Complete step by step solution:
A loaded beam has two loads in downward direction, and it is still stationary means a force of the same magnitude but in the opposite direction helps this beam to be stationary.
Firstly we will calculate total downward load given on the beam.
 $ {L_{Total}} = {L_1} + {L_2} $
Put values of $ {L_1} $ and $ {L_2} $ in above equation
 $ {L_{Total}} = 60 + 40 = 100KN $
Here, we got the total load on the beam in a downward direction that is $ 60KN $ , means $ 60KN $ force is also applied in an upward direction.
So, let the first support in upward direction $ = {U_1} $
And second support in upward direction $ = {U_2} $
Total support in upward direction $ = {U_{Total}} $
 $ $ $ {U_{Total}} = {U_1} + {U_2}......1 $
As per question we can give two supports on $ A $ and $ B $ to keep this beam stationary, and the magnitude of that force we have already calculated.
Hence, $ {U_{Total}} = {L_{Total}} $
Both upward support should be equal.
So, $ {U_1} = {U_2} $
Now, equation 1 can be written as
 $ {U_{Total}} = {U_1} + {U_1} $
 $ {U_{Total}} = 2{U_1} = 100KN $
 $ \Rightarrow {U_1} = {U_2} = \dfrac{{100KN}}{2} = 50KN $
Here, two supports of $ 50KN $ strength will act upward on $ A $ and $ B $ to balance the beam.

Note:
We should know the concept of equilibrium to solve the above question. In equilibrium, a beam is supported by force at both ends, all the download loads are balanced by equal and opposite upward forces and the beam gets stationary.