Question

Determine the position of the point on the rod which remains stationary immediately after collision.
(A) The point is a distance $\left( \dfrac{1}{3} \right)l$ from the end where the mass strikes.
(B) The point is a difference $\left( \dfrac{2}{3} \right)l$ from the end where the mass strikes.
(C ) The point is a distance $\left( \dfrac{2}{5} \right)l$ from the end where the mass strikes.
(D) The point is a difference $\left( \dfrac{1}{5} \right)l$from the end where the mass strikes.

Answer 1

Hint: Apply the concept of collision in one dimension. Consider a point A where the velocity is zero. When two of the objects collide with each other the total momentum before collision is equal to the momentum after collision in the absence of external forces. That is the law of conservation of momentum.

Complete answer:

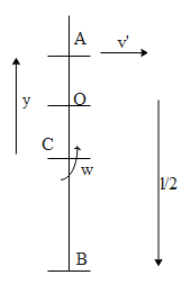
Let the point at rest be A.
That is, ${{V}_{A}}=0$
$\begin{align}
  & v'-yw=0 \\
 & \Rightarrow \dfrac{v}{3}-y\dfrac{v}{l}=0 \\
 & \Rightarrow \dfrac{v}{3}=y\dfrac{v}{l} \\
\end{align}$
Cancelling v on both sides of the equation we get,
$\dfrac{1}{3}=\dfrac{y}{l}$
$\Rightarrow y=\dfrac{l}{3}$
Thus, $BA=\dfrac{l}{3}+\dfrac{l}{3}=\dfrac{2l}{3}$

$\therefore $ option (B) is correct.

Additional information:
Let us consider two particles of masses ${{m}_{1}}$ and ${{m}_{2}}$ moving with velocities ${{u}_{1}}$ and ${{u}_{2}}$ respectively before collision. If there velocities after collision are ${{v}_{1}}$ and ${{v}_{2}}$, then according to conservation of momentum we have,
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Here, the initial and final positions are widely separated so that the interaction forces between the particles becomes effectively zero. Hence the potential energy before and after remains the same. If the collision is perfectly elastic, the total kinetic energy of the particles is not changed by the collision.
$\dfrac{1}{2}{{m}_{1}}u_{1}^{2}+\dfrac{1}{2}{{m}_{2}}u_{2}^{2}=\dfrac{1}{2}{{m}_{1}}v_{1}^{2}+\dfrac{1}{2}{{m}_{2}}v_{2}^{2}$
According to the kinetic theory of gases, such elastic collision occurs between the molecules of a gas. This type of collision mostly takes place between atoms, electrons and protons.
In case of inelastic collision, some of the kinetic energy is converted to other forms of energy. This energy can be in the form of thermal energy in macroscopic particles.

Note:
When two identical materials collide together, in one dimension their kinetic energy as well as momentum is conserved after collision. Maximum energy loss occurs when the particles strike together as a result of collision. The collision imparts force in the line of collision, the collision does not change the velocities that are tangent to the point of collision. The velocities in the line of collision can be used as the same one dimensional equation.