Question

Determine the minimum height of a vertical flat mirror in which a person is $178{\text{ cm}}$ tall and can see his or her full image.

Answer 1

Hint: To solve such problems related to mirrors we should always consider drawing a ray diagram. Here we are given the height of the man and we need to find the length of the mirror which is required if the man wishes for its full image on the flat mirror.

Complete step by step answer:
We will draw a diagram to get a clear picture of the situation in the question.

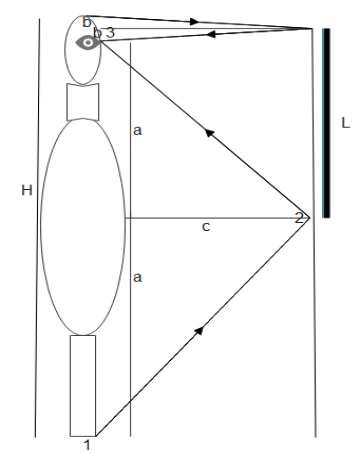
So as we can see in the diagram there are two rays, one from the head of the man of height $H$ and one from the foot of the man striking the mirror of length $L$ at the point $2$. These two rays will bounce back at the same angle meeting at the eye of the man at the point $3$ so that the man can see his full image on the mirror.

Therefore the distance between the ray from the head and the reflected ray will be $2b$ and that of the ray from the foot will be $2a$. So the height of the man $H = 2a + 2b$.
And as from the diagram, we can see that the length of the mirror is $L = a + b$
$ \Rightarrow L = \dfrac{H}{2}$
Substituting the value of $H$ we get
$ \therefore L = 89{\text{ cm}}$
Therefore a mirror of length half of the height of the man will be needed so that the man standing in front of it can see his full image in the mirror.

Note: The image formed by a flat or a plane mirror is always virtual (means the light rays do not come from the image). The image is laterally inverted and is erect. The size of the image is the same as the size of the object and the distance between the image is the same as the distance between the object from the mirror.