Question

Determine the length of chord, which is at a distance of 7 cm from the circle of radius 25cm.
$\left( a \right)$ 25cm
$\left( b \right)$ 48cm
$\left( c \right)$ 16cm
$\left( d \right)$ 24cm

Answer 1

Hint: In this particular question use the concept that the line joining the center and any point of the circumference is nothing but the radius of the circle, so every chord of the circle touches the circle at two points jo join one of the point of the chord to the center of the circle and draw the perpendicular from the center of the circle on the given chord, so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Given data:
Chord is at 7 cm from the circle.
Therefore the shortest distance of the chord from the center of the circle is 7 cm.
Radius of the circle = 25 cm.
Let us consider a circle with center O, and a chord AB as shown in the below figure, join O and A which is the radius of the circle and draw the perpendicular from the center of the circle on the given chord which cuts the chord at point C , so OC = 7 cm as shown in the below figure.

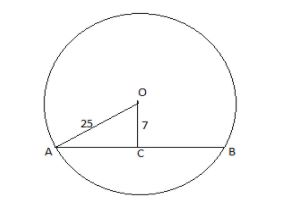
Now as we see that OC is perpendicular to AB, therefore, $\angle OCA = {90^o}$.
So in triangle AOC apply Pythagoras theorem we have,
As we know that according to the Pythagoras theorem that in a right triangle the sum of the square of the base and perpendicular is equal to the square of the hypotenuse.
$ \Rightarrow {\left( {{\text{base}}} \right)^2} + {\left( {{\text{perpendicular}}} \right)^2} = {\left( {{\text{hypotenuse}}} \right)^{^2}}$................. (1)
So in triangle AOC we have,
Base = AC, perpendicular = OC, and hypotenuse = OA.
So from equation (1) we have,
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{OC}}} \right)^2} = {\left( {{\text{OA}}} \right)^{^2}}$
Now substitute the values we have,
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} + {\left( {\text{7}} \right)^2} = {\left( {{\text{25}}} \right)^{^2}}$
$ \Rightarrow {\left( {{\text{AC}}} \right)^2} = 625 - 49 = 576 = {\left( {24} \right)^2}$
$ \Rightarrow {\text{AC}} = 24$ cm
Now OC is also the bisector of the chord so AB = 2 (AC)
Therefore, the length of chord AB = 2 (24) = 48 cm.
So this is the required length of the chord AB.

So, the correct answer is “Option B”.

Note: Whenever we face such types of question the key concept we have to remember is that always recall the Pythagoras theorem which is stated above then simplify substitute the values as above and simplify we will get the half the length of the chord, then double it we will get the required length of the chord AB.