Question

How do you determine the exact coordinates of a point on the terminal arm of the angle in standard position given 45 degree

Answer 1

Hint: This type of problem is based on the concept of relation between Cartesian and polar coordinates. First, consider the point to be P. Now, we know that the relation between the cartesian and polar coordinates are \[x=r\cos \theta \]and \[y=r\sin \theta \]. To find P(x,y), we have to know the values of \[\theta \] and r. we have been given \[\theta \]=45 degrees.

Complete step-by-step solution:
Consider the point to be in a unit circle with radius r=1. On substituting the values of r and \[\theta \], we can find the values of x and y with the help of the trigonometric table which is the required answer.
According to the question, we are asked to find the Cartesian coordinates of the terminal arm of the angle in standard position with 45 degree.
We have been given the angle is 45 degrees.
We know that the relation between the relation between Cartesian and polar coordinates are \[x=r\cos \theta \]and \[y=r\sin \theta \].
Here, \[\theta \] is the angle obtained by the point and r is the distance between the origin and the point.
Let us plot a graph to understand better.

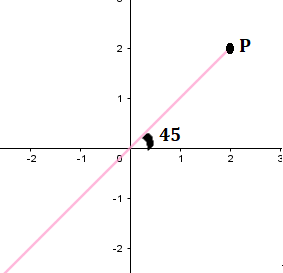
We know that \[\theta \]=45 degrees which can be represented as \[\dfrac{\pi }{4}\].
Let us find the sine and cosine values of \[\dfrac{\pi }{4}\].
We know that \[\sin \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\] and \[\cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\].
Substituting these values in (1) and (2), we get
\[x=r\dfrac{1}{\sqrt{2}}\] and
\[y=r\dfrac{1}{\sqrt{2}}\].
We know that r is equal to the radius of a unit circle.
Therefore, we get r=1.
On substituting r in the expression, we get
\[x=\dfrac{1}{\sqrt{2}}\] and \[y=\dfrac{1}{\sqrt{2}}\].
Therefore, the coordinate of the point P is \[\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right)\].
Hence, the coordinate of the point on the terminal arm of the angle in the standard position with 45-degree angle is \[\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right)\].

Note: We can further simplify the obtained solution.
Multiply \[\sqrt{2}\] on both the numerator and denominator of the coordinates.
We get \[\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right)=\left( \dfrac{1\sqrt{2}}{\sqrt{2}\sqrt{2}},\dfrac{1\sqrt{2}}{\sqrt{2}\sqrt{2}} \right)\].
On further simplification, we get
\[\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right)=\left( \dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} \right)\]
We can also represent the answer in this form also.