Question

How do you determine the amplitude, period, and shifts to the graph \[y=2\cos x\]?

Answer 1

Hint: The standard form of the cosine function is \[y=a\cos \left( bx+c \right)+d\], here a, b, c, and d \[\in \]Real numbers. For this equation, the amplitude is \[\left| a \right|\], period is \[\dfrac{2\pi }{b}\], phase shift is \[\dfrac{-c}{b}\], and vertical shift is d. By comparing the coefficients of the equation, we can find the a, b, c, d, and thus amplitude, period, and shifts can also be found.

Complete step by step answer:
We are given the cosine function \[y=2\cos x\]. We have to find its amplitude, period, and shifts. The standard form of the cosine function is \[y=a\cos \left( bx+c \right)+d\]. Comparing the given cosine equation with standard form we get, \[a=2,b=1,c=0,\] and \[d=0\].
We can find the amplitude, period, horizontal/phase shift, and vertical shift from these as follows,
Amplitude of given equation is \[\left| a \right|=\left| 2 \right|=2\], period of the given equation is \[\dfrac{2\pi }{b}=\dfrac{2\pi }{1}=2\pi \], horizontal/ phase shift of the equation is \[\dfrac{-c}{b}=\dfrac{0}{1}=0\], and vertical shift of equation is d \[=0\].
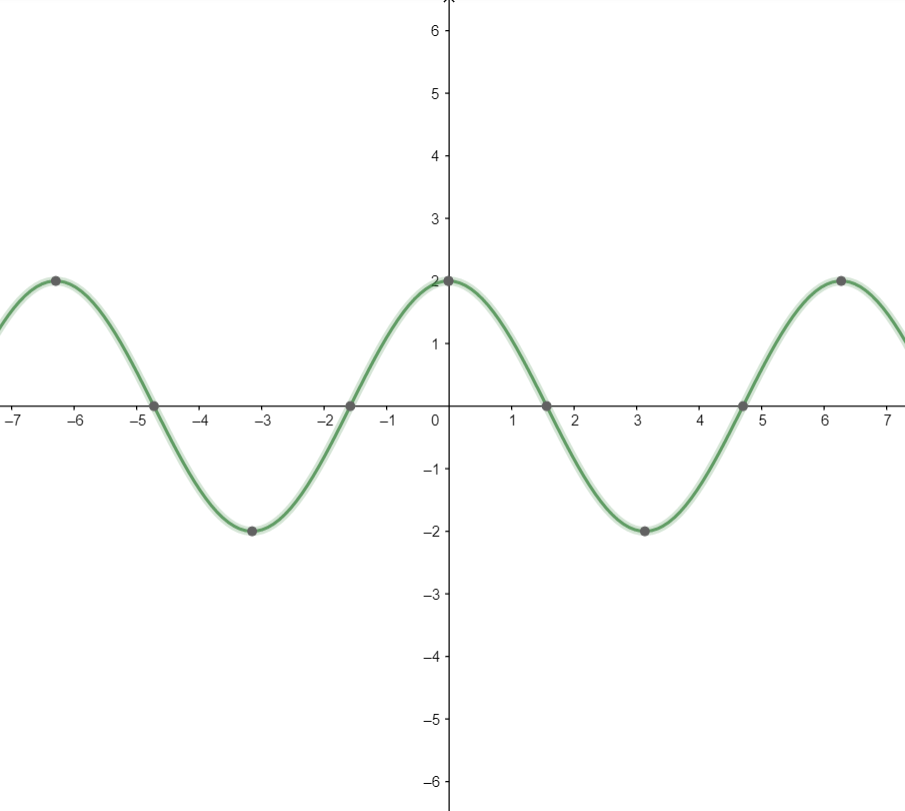
Hence the amplitude, period, horizontal/ phase shift, and vertical shift of the given equation are \[2,2\pi ,0\], and \[0\] respectively.
Using this we can also plot the graph for the given cosine function as,
      

Note:
Similar type of question can be asked for sine functions also, for that we should know what the standard form of sine function is: \[y=a\sin \left( bx+c \right)+d\]. Same as for cosine function here also a, b, c, and d \[\in \]Real numbers. For this equation, the amplitude is \[\left| a \right|\], period is \[\dfrac{2\pi }{b}\], phase shift is \[\dfrac{-c}{b}\], and vertical shift is d.