Question

How do you determine ordered pairs are part of the solution set of inequalities \[3x+y\le 6\] for \[\left( 4,3 \right),\left( -2,4 \right),\left( -5,-3 \right),\left( 3,-3 \right)\]?

Answer 1

Hint: Inequalities do not provide a fixed value as a solution; it gives a range. All the values in this range hold the inequality. For this question, as this is a linear inequality in two variables, we can not solve it using only this equation. So, we will substitute the values for the given coordinates of points. If the inequality is satisfied then the pair is part of the solution set.

Complete step by step answer:
We are asked to determine if the ordered pairs are the part of the solution set of inequality \[3x+y\le 6\].
Substituting the first ordered pair \[\left( 4,3 \right)\] in inequality, we get
\[\begin{align}
  & 3\times 4+3\le 6 \\
 & 15\le 6 \\
\end{align}\]
But this is not true, this pair does not belong to the solution set.
Substituting the next ordered pair \[\left( -2,4 \right)\] in inequality, we get
\[\begin{align}
  & 3\times (-2)+4\le 6 \\
 & -2\le 6 \\
\end{align}\]
This is true, so this pair belongs to the solution set.
Substituting the next ordered pair \[\left( -5,-3 \right)\] in inequality, we get
\[\begin{align}
  & 3\times (-5)-3\le 6 \\
 & -18\le 6 \\
\end{align}\]
This is true, so this pair belongs to the solution set.
Substituting the next ordered pair \[\left( 3,-3 \right)\] in inequality, we get
\[\begin{align}
  & 3\times 3-3\le 6 \\
 & 6\le 6 \\
\end{align}\]
This is true, so this pair belongs to the solution set.

Thus, the ordered pairs that are part of the solution set are \[\left( -2,4 \right),\left( -5,-3 \right),\left( 3,-3 \right)\].

Note: We can also use a different method to solve the given question. Here, we will plot the graph of \[3x+y=6\]. Then, all the values that lie below the graph of this equation belong to the solution set of the inequality \[3x+y\le 6\].
Thus, we get
 

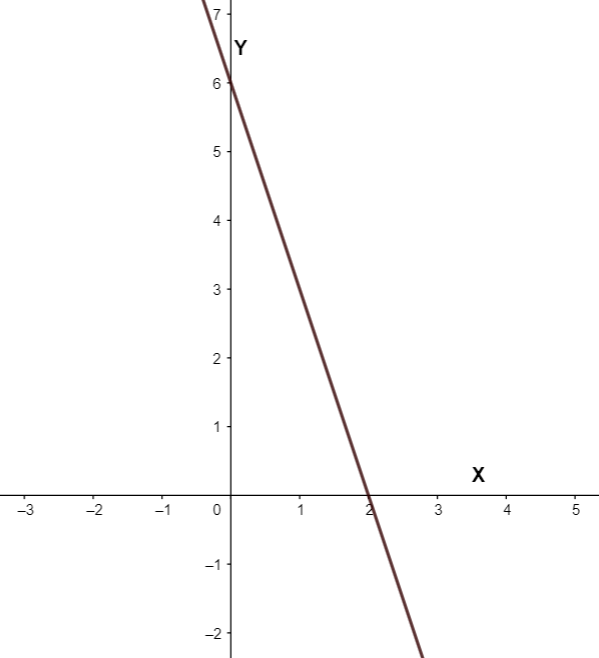
Thus, all points that lie below the graph in the above figure satisfy the given inequality.