Question

How to determine height of the cylinder with maximum volume engraved in a sphere with radius $ R $ ?

Answer 1

Hint: We have to determine the height of the cylinder with maximum volume engraved in a sphere with radius $ R $ , its cross-sectional area and height are restricted by the sphere , we know that volume of a cylinder is given by $ V = \pi {r^2}h $ . For maximum volume , $ \dfrac{{dV}}{{dh}} = 0 $ .

Complete step-by-step answer:
Consider a cylinder, however, is engraved in a sphere, its cross-sectional area and height are restricted by the sphere and when the sphere cut vertically then we get the required cross-section as shown below ,

                

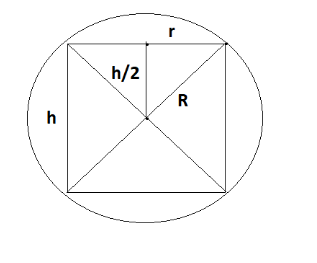
In the above figure ,
‘h’ is the height of the cylinder ,
‘r’ is the radius of the cylinder,
And ‘R’ is the radius of the sphere.
By applying Pythagoras Theorem , we will get the relationship between height of the cylinder, radius of the cylinder, radius of the sphere.
Therefore, we get the following,
 $ \Rightarrow {R^2} = {\left( {\dfrac{h}{2}} \right)^2} + {r^2} $
Now, simplifying the above equation, we will get ,
 $ \Rightarrow {R^2} = \dfrac{{{h^2}}}{4} + {r^2} $
For solving radius of the cylinder that is $ r $ , we will get ,
 $ \Rightarrow {r^2} = {R^2} - \dfrac{{{h^2}}}{4}.......(1) $
Volume of a cylinder , $ V = \pi {r^2}h $ . (original equation)
Now substitute $ (1) $ in our original equation ,
We will get,
 $ V = \pi {r^2}h $
 $ = \pi \left( {{R^2} - \dfrac{{{h^2}}}{4}} \right)h $
 $ = \pi {R^2}h - \dfrac{{{h^3}}}{4} \pi $
For maximum volume , we can write ,
 $ \Rightarrow \dfrac{{dV}}{{dh}} = 0 $
 $ \Rightarrow \dfrac{d}{{dh}}\left( {\pi {R^2}h - \dfrac{{{h^3}}}{4}}\pi \right) = 0 $
 $ \Rightarrow {R^2} - \dfrac{3}{4}({h^2}) = 0 $
We have to solve for height of the cylinder that is $ h $ ,
Subtract $ {R^2} $ from both the side,
\[
   \Rightarrow {R^2} - {R^2} - \dfrac{3}{4}({h^2}) = - {R^2} \\
   \Rightarrow - \dfrac{3}{4}{h^2} = - {R^2} \;
 \]
After simplifying ,
\[ \Rightarrow \dfrac{3}{4}{h^2} = {R^2}\]
Now multiple by $ \dfrac{4}{3} $ both the side of the equation, we will get ,
\[ \Rightarrow {h^2} = \dfrac{4}{3} {R^2}\]
Now, taking square root both the side,
 $ \Rightarrow h = \sqrt {\dfrac{4}{3} } R $
We get the required result.
So, the correct answer is “ $ \Rightarrow h = \sqrt {\dfrac{4}{3}} R $ ”.

Note: The important thing to recollect about any equation is that the ‘equals’ sign represents a balance. What the sign says is that what’s on the left-hand side is strictly an equal to what’s on the right-hand side. It is the type of question where only mathematical operations such as addition, subtraction, multiplication and division is used.