Question

Derive the Fourier`s conduction equation for general bodies.

$\left( {\dfrac{{dq}}{{dt}} = - kA\dfrac{{dt}}{{dx}}} \right)$

Answer 1

Hint: Fourier law of heat conduction is the governing law for conduction equations. It states that the rate of heat transfer is directly proportional to the area normal to the direction of heat flow and temperature gradient i.e., drop in temperature per unit length.

Complete solution:
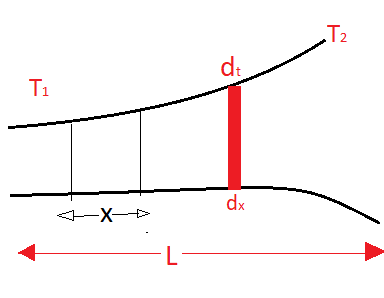
Let us consider a small elemental area from the above body

Let the width of this elemental part be $dx$
The small change in temperature be $dt$
A temperature gradient will be the change in temperature per unit area or $\dfrac{{dt}}{{dx}}$
And let $A$ be the area perpendicular to the direction of heat flow
Refer to the diagram
Now as per Fourier’s law
$\dfrac{{dq}}{{dt}} \propto {\rm A}$and,
$\dfrac{{dq}}{{dt}} \propto \dfrac{{dt}}{{dx}}$
$\therefore \dfrac{{dq}}{{dt}} \propto {\rm A}\dfrac{{dt}}{{dx}}$
$\dfrac{{dq}}{{dt}}$ is the rate of heat transferred?
Here to remove the proportionality a constant of proportionality is inserted which
$k$ which is known as Thermal conductivity of the material or wall and is expressed in $\left( {\dfrac{w}{m}K} \right)$
$\therefore \dfrac{{dq}}{{dt}} = - kA\dfrac{{dt}}{{dx}}$
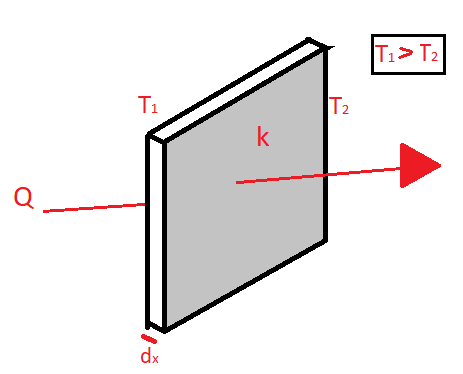
Here the negative sign indicates the drop in temperature across the body
Since $dt$ is the change in temperature so it will be expressed as
$dt = {T_2} - {T_1}$
And as it is evident that ${T_2}$ will be lower than ${T_1}$ so we`ll get a negative value of $dt$ so we use a negative sign before $k$ to nullify this and make heat transfer rate positive

The heat flow rate $\dfrac{{dq}}{{dt}}$ across a body will be $\dfrac{{dq}}{{dt}} = - kA\dfrac{{dt}}{{dx}}$.

Note: The heat always flows from higher temperature to lower temperature that’s why ${T_1}$ will always be greater than ${T_2}$.
The area perpendicular to heat flow rate will always be considered because it is the only area which will cause resistance to the flow of heat and thus will reduce its temperature.
The thermal conductivity $\left( k \right)$is the internal property of the body; it is the measure of how easily heat can be conducted through a body. It is generally higher for metals and lowers for non-metals .