Question

Derive the formula for the curved surface area and the total surface area of the frustum of a cone. \[\]

Answer 1

Hint: We cut the cone ABC with a parallel to the circular base BC at the points D, E, and obtain the frustum of the cone DBCE. We drop perpendicular which meets base at the top at Q and base at the bottom at P. We express the slant height of the cone ADE in terms of slant heights of frustum DCBE $l$, the radius of the top base ${{r}_{2}}$ and the radius of the bottom base ${{r}_{1}}$ using the similarity of the triangles ABP and ADQ. We use the fact that the curved surface area of the frustum is the difference between curved surface areas of the cones ABC and ADE.\[\]

Complete step-by-step solution:

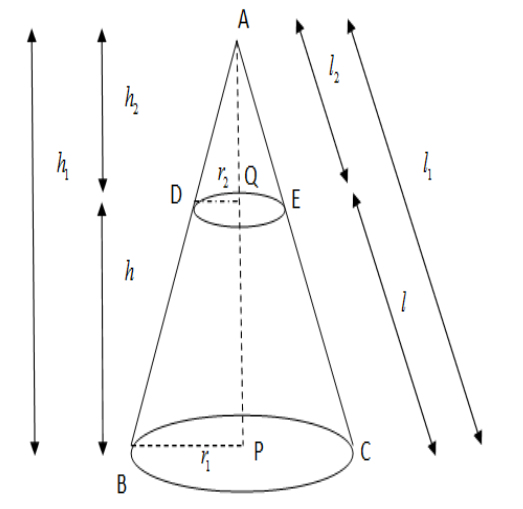
Let ABC be a cone where A is the vertex or apex of the cone and B,C be two points on the edge of the circular base at the bottom. We cut the cone with a plane parallel to the plane containing the circular base at the bottom and the point of intersection of the plane is D and E. We obtain the frustum of the cone DBCE with D, E two points on the edge of circular base at the top. \[\]
We drop perpendicular from the apex A which meets the top circular base at the point M and the bottom circular base at the point N. Let us denote the height of the cone ABC as ${{h}_{1}}$ and slant height as ${{l}_{1}}$, the radius at the bottom circular base as ${{r}_{1}}$. So we have
\[AB=AC={{l}_{1}},AP={{h}_{1}},PB={{r}_{1}}\]
Let us denote the radius at the top circular base of the frustum of the cone DBCE as ${{r}_{2}}$ , the height as $h$, and slant height $l$. So we have
\[QD={{r}_{2}},QP=h,BD=EC=l\]
We see that in the frustum of a cone we can only know $h,l,{{r}_{1}},{{r}_{2}}$. So we observe the smaller cone ADE which is not a part of frustum and denote its height as ${{h}_{2}}=AQ$ and its slant height ${{l}_{2}}=AD$. We have
\[\begin{align}
  & {{l}_{2}}=AD=AB-BD \\
 & \Rightarrow {{l}_{2}}={{l}_{1}}-l \\
 & \Rightarrow {{l}_{1}}=l+{{l}_{2}}.....\left( 1 \right) \\
\end{align}\]
We observe that the curved surface area of the frustum of the cone is the difference between the curved surface area of the original cone ABC and the smaller cone ADE which is not a part of frustum. So we have the curved surface area of the frustum DBCE
\[\begin{align}
  & \text{CSA}=\text{CSA of cone ABC}-\text{CSA of cone ADE} \\
 & \Rightarrow \text{CSA=}\pi \times {{r}_{1}}\times {{l}_{1}}-\pi \times {{r}_{2}}\times {{l}_{2}}....\left( 2 \right) \\
\end{align}\]
Let us observe the triangles ADQ and ABP. We have $\angle AQD=\angle APB={{90}^{\circ }}$, the common angle $\angle BAP=\angle DAQ$ which gives us $\angle ADQ=\angle ABP$. SO by angle-angle-angle similarity we have
\[ADQ\sim ABP\]
So the ratio of the respective side will be equal. We have
\[\begin{align}
  & \dfrac{QD}{PB}=\dfrac{AQ}{AP}=\dfrac{AD}{AB} \\
& \Rightarrow \dfrac{{{r}_{2}}}{{{r}_{1}}}=\dfrac{{{h}_{2}}}{{{h}_{1}}}=\dfrac{{{l}_{2}}}{{{l}_{1}}} \\
\end{align}\]
We have to convert ${{l}_{1}},{{l}_{2}}$ in terms of $l$ as we need only surface area. We replace ${{l}_{1}}$ using the equation (1) and have
\[\begin{align}
  & \dfrac{{{r}_{2}}}{{{r}_{1}}}=\dfrac{{{l}_{2}}}{l+{{l}_{2}}} \\
 & \Rightarrow {{r}_{2}}\left( l+{{l}_{2}} \right)={{r}_{1}}{{l}_{2}} \\
 & \Rightarrow {{r}_{2}}l={{l}_{2}}\left( {{r}_{1}}-{{r}_{2}} \right) \\
 & \Rightarrow {{l}_{2}}=l\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\
\end{align}\]
We put the above obtained value in equation in (2) and have,
\[\begin{align}
  & \text{CSA=}\pi \times {{r}_{1}}\times {{l}_{1}}-\pi \times {{r}_{2}}\times {{l}_{2}} \\
 & =\pi {{r}_{1}}\left( l+{{l}_{2}} \right)-\pi {{r}_{2}}{{l}_{2}}\left( \because {{l}_{1}}=l+{{l}_{2}} \right) \\
 & =\pi {{r}_{1}}\left( l+l\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \right)-\pi {{r}_{2}}l\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\
\end{align}\]
We take $l$ outside the bracket and have,
\[\begin{align}
  & =\pi {{r}_{1}}l\left( 1+\dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right)-\pi {{r}_{2}}l\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\
 & =\pi {{r}_{1}}l\left( \dfrac{{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}} \right)-\pi {{r}_{2}}l\left( \dfrac{{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right) \\
 & =\pi l\left( \dfrac{{{r}_{1}}^{2}-{{r}_{2}}^{2}}{{{r}_{1}}-{{r}_{2}}} \right) \\
\end{align}\]
We use the algebraic identity ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$ and have
\[\begin{align}
  & =\pi l\left( \dfrac{\left( {{r}_{1}}-{{r}_{2}} \right)\left( {{r}_{1}}+{{r}_{2}} \right)}{{{r}_{1}}-{{r}_{2}}} \right) \\
 & =\pi l\left( {{r}_{1}}+{{r}_{2}} \right) \\
\end{align}\]
So the curved surface area is found to be \[\text{CSA}=\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\]. The total surface area is the sum of curved surface area CSA, the area of the top circular base ${{A}_{t}}$ and bottom circular base ${{A}_{b}}$. We have the area of the bases as
\[{{A}_{t}}=\pi {{r}_{1}}^{2},{{A}_{b}}=\pi {{r}_{2}}^{2}\]
So the total surface area TSA of the frustum of the cone is
\[\text{TSA}=\text{CSA}+{{A}_{t}}+{{A}_{b}}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi {{r}_{1}}^{2}+\pi {{r}_{2}}^{2}\]

Note: We note that the other obtained ratio $\dfrac{{{r}_{2}}}{{{r}_{1}}}=\dfrac{{{h}_{2}}}{{{h}_{1}}}$ can be used to find the volume of the frustum of the cone which is given by $V=\dfrac{1}{3}\pi h\left( {{r}_{1}}^{2}+{{r}_{1}}{{r}_{2}}+{{r}_{2}}^{2} \right)$. We can also find the curved surface area in terms of height $h$ of the frustum using Pythagoras theorem as $A=\pi \left( {{r}_{1}}+{{r}_{2}} \right)\sqrt{{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}-{{h}^{2}}}$.