Question

Derive the expression for the magnetic field due to a current-carrying coil of the radius $r$ at a distance $x$ from the center along $X - axis$.

Answer 1

Hint: We will calculate the magnetic field due to a current-carrying coil of radius $r$ at a distance $x$ from the center of along $X - $ axis by using BIOT-SAVART’S LAW. We can also say that it is the application of BIOT-SAVART LAW.

Complete step by step answer:
Here, we will use BIOT-SAVART’S LAW to calculate the magnetic field due to a current-carrying loop.
For this, we will consider a circular loop, which is a plane circular ring of a conducting wire.

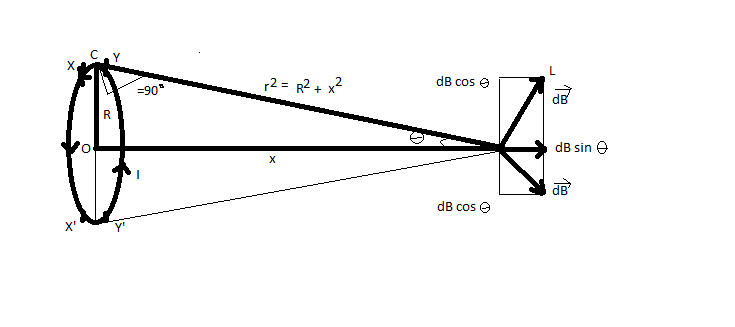
Now, let P be the point on the axis of the circular loop or coil, where the magnetic field is to be calculated. Here, $R$ is the radius of a current-carrying loop and $x$ is the distance of point P from the center of the coil.
Let XY be a small element of length $dl$ at a distance $r$from point P. We know that every current element is perpendicular to $\hat r$.
Now, according to BIOT-SAVART’S LAW, magnetic field due to a small element XY at point P is given by
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,dl\,\sin \phi }}{{{r^2}}}.$

Since, $\phi = 90^\circ $, as shown in the figure, therefore, the above equation can be written as
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,dl\,\sin 90^\circ }}{{{r^2}}}$
$ \Rightarrow $ $dB = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{I\,dl}}{{{r^2}}}$

Now, from the above equation, we can say that the direction of $d\vec B$ is perpendicular to the plane formed by $d\vec l$ and $\vec r$ and is along PL which is perpendicular to PC.

Now, we will resolve $dB$ into two components and is given by
i) $dB\,\cos \theta $, which is perpendicular to the axis of the coil and
ii) $dB\,\sin \theta $, which is along the axis of the coil and away from the center of the coil.

Now, we can see that the $dB\,\sin \theta $ component of the magnetic field due to each element of the coil or loop is directed in the same direction. Therefore, the magnetic field at P due to the whole coil or loop is equal to the sum of the $dB\,\sin \theta $ component of the magnetic field due to each element.
i.e. $B = \sum {dB\,\sin \theta } $ or $B = \int {dB\,\sin \theta } $
Now, putting the value of $dB$in the above equation we get,
$B = \int {\dfrac{{{\mu _0}I\,dl}}{{4\pi {r^2}}}\sin \theta } $
$ \Rightarrow $ $B = \dfrac{{{\mu _0}I\,\sin \theta }}{{4\pi {r^2}}}\int {dl} $
Here, $I$, $\theta $ and $r$ are constant.

Also, $\int {dl = } $ the length of the circular coil $ = $ the circumference of the coil $ = 2\pi R$.
Therefore, $dB = \dfrac{{{\mu _0}I\,\sin \theta \times 2\pi R}}{{4\pi {r^2}}}$
Now, from the figure, we can say that
$\sin \theta = \dfrac{R}{r}$
Putting this value, we get
$B = \dfrac{{{\mu _0}I}}{{4\pi {r^2}}}\,\dfrac{{R\,2\pi R}}{r}$
$ \Rightarrow \,B = \dfrac{{{\mu _0}}}{{4\pi }}(\dfrac{{2\pi I{R^2}}}{{{r^3}}})$
But, $r = \sqrt {{R^2} + {x^2}} $

Therefore $\,\,B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{2\pi I{R^2}}}{{{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}$, Which is the magnetic at the axis of the current-carrying loop.

Additional Information:
Now, if we consider a case in which the observation point P is far away from the loop or coil (i.e. $x \gg \,R$), then we can neglect the ${R^2}$ as compared to the ${x^2}$.
Hence, ${\left( {{R^2} + {x^2}} \right)^{\dfrac{3}{2}}} = {x^3}$
Therefore, the equation of magnetic field becomes
$B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{2\pi I{R^2}}}{{{x^3}}}$
Since, area of loop, $A = \pi {R^2}$
Therefore $\,B' = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{2IA}}{{{x^3}}}.$

Note: We can also calculate magnetic if the coil has $N$ turns which is given by
$B = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{2\pi NI{R^2}}}{{{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}$
And $B' = \dfrac{{{\mu _0}}}{{4\pi }}\,\dfrac{{2\pi NI}}{R}$.