Question

How do you derive the area formula for a parallelogram?

Answer 1

Hint: At first, we divide the parallelogram into two triangles by joining any two opposite vertices. These two triangles are exactly the same (congruent) and thus have equal areas. The area of the parallelogram is the summation of the individual areas of the two triangles. We drop a perpendicular from a vertex to its opposite side to get an expression for the height of the triangles. The area of the individual triangle is $\dfrac{1}{2}\times base\times height$ .The area of the parallelogram being twice the area of the triangle, thus becomes after evaluation $base\times height$ .
Complete step by step answer:
The parallelogram can be divided into two triangles by constructing a diagonal by joining any two opposite vertices.

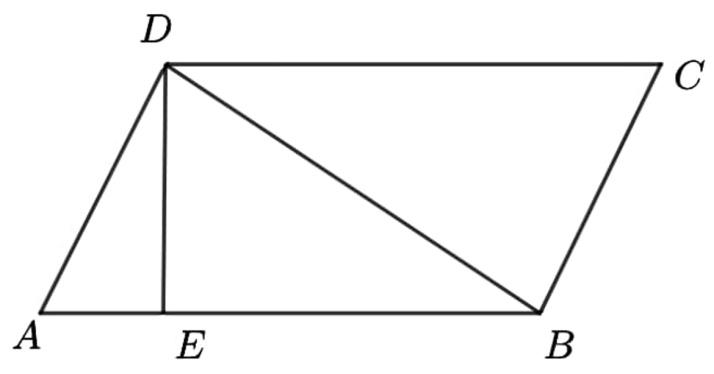
In the above figure, $\Delta ABD$ and $\Delta BCD$are the two such triangles. These two triangles have:
$AB=CD$ (as opposite sides of a parallelogram are equal)
$AD=BC$ (opposite sides of a parallelogram are equal)
$BD$ is common
Thus, the two triangles are congruent to each other by SSS axiom of congruence. Since, the areas of two congruent triangles are equal,
$\Rightarrow area\left( \Delta ABD \right)=area\left( \Delta BCD \right)$
Now, we need to find the area of $\Delta ABD$ . We draw a perpendicular from $D$ to the side $AB$ and name it as $DE$ . Thus, $\Delta ABD$ is now a triangle with base $AB$ and height $DE$ .
Then, the area of the $\Delta ABD$ becomes
$area\left( \Delta ABD \right)=\dfrac{1}{2}\times base\times height$
$\Rightarrow area\left( \Delta ABD \right)=\dfrac{1}{2}\times AB\times DE$
The area of $\Delta BCD$ being equal to that of $\Delta ABD$ is also $\dfrac{1}{2}\times AB\times DE$ .
The area of the parallelogram $ABCD$ is the summation of the areas of the two triangles, which is
$\Rightarrow area\left( ||gmABCD \right)=2\times \dfrac{1}{2}\times AB\times DE$
$\Rightarrow area\left( ||gmABCD \right)=AB\times DE$
It is to be noted that the perpendicular $DE$ is also the height of the parallelogram $ABCD$ and the base $AB$ is also the base of the parallelogram $ABCD$ .
Thus, we can write the general expression of the formula of the area of a parallelogram as
$area\left( ||gmABCD \right)=base\times height$
Where $base$ indicates any one of the sides and $height$ indicates the perpendicular distance between this side and its opposite side.

Note: Students must be careful while drawing the perpendicular and must remember that perpendicular must be drawn from the opposite side to the side taken as base. Area of a parallelogram can also be derived by assuming any two adjacent sides of it as two vectors say $\vec{a}$ and $\vec{b}$ . Then, the area becomes
$area\left( ||gmABCD \right)=\vec{a}\times \vec{b}$