Question

Derive expression for terminal velocity when a ball of radius $r$ is dropped through a liquid of viscosity $\eta $ and density $\rho $.

Answer 1

Hint: The constant value of speed that a freely falling body acquires, when the resistance of the medium through which it is falling prevents further acceleration of the body, is called as terminal velocity of the body. In order to calculate the terminal velocity of a body in a liquid of density $\rho $, we need to apply Stoke’s law and balance the downward gravitational force of the body with the sum of upthrust and viscous force acting on the body.

Complete step-by-step answer:
Terminal velocity is defined as the highest velocity attained by a body that is falling through a fluid. It is observed when the sum of drag force and buoyant force becomes equal to the downward gravitational force that is acting on the body. The acceleration of the body is zero as the net force acting on the body is zero.
Viscous drag or viscous force acts in the direction opposite to the motion of the body in the fluid. According to Stoke’s law, the magnitude of the opposing viscous drag increases with the increasing velocity of the body.
As the body falls through a medium, its velocity goes on increasing due to the force of gravity acting on it. Thus, the opposing viscous or drag force, which acts upwards, also goes on increasing. A stage reaches when the true weight of the body is just equal to the sum of the upward thrust due to buoyancy, that is, upthrust, and the upward viscous drag. At this stage, there is no net force to accelerate the moving body. Hence it starts falling with a constant velocity, which is called terminal velocity.

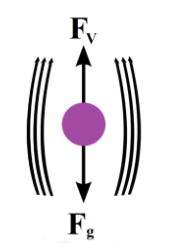
Let ${{\rho }_{o}}$ be the density of the material of the spherical body, ball of radius $r$ and $\rho $ be the density of the medium.
True weight of the body is given as,
$W=\text{Volume}\times \text{Density}\times g$
Volume of spherical body is, $V=\dfrac{4}{3}\pi {{r}^{3}}$
Where,
$r$ is the radius of the ball
Therefore,
$W=\dfrac{4}{3}\pi {{r}^{3}}{{\rho }_{o}}g$
Where,
$r$ is the radius of the ball
${{\rho }_{o}}$ is the density of the material of the ball
Now,
Let’s say ${{F}_{T}}$ is the weight of the liquid displaced
${{F}_{T}}=\text{Volume of liquid displaced }\times \text{ Density }\times g$
Or,
${{F}_{T}}=\dfrac{4}{3}\pi {{r}^{3}}\rho g$
Where,
$r$ is the radius of the ball
$\rho $ is the density of the material
$g$ is the acceleration due to gravity
If $v$ is the terminal velocity of the body, then according to Stoke’s law,
Upward viscous drag is given as,
${{F}_{V}}=6\pi \eta rv$
Where,
$r$ is the radius of the ball
$\eta $ is the viscosity of the liquid
When the body acquires terminal velocity,
${{F}_{T}}+{{F}_{V}}=W$
Putting values,
$\begin{align}
  & {{F}_{T}}=\dfrac{4}{3}\pi {{r}^{3}}\rho g \\
 & {{F}_{V}}=6\pi \eta rv \\
 & W=\dfrac{4}{3}\pi {{r}^{3}}{{\rho }_{o}}g \\
\end{align}$
We get,
$\begin{align}
  & \dfrac{4}{3}\pi {{r}^{3}}\rho g+6\pi \eta rv=\dfrac{4}{3}\pi {{r}^{3}}{{\rho }_{o}}g \\
 & 6\pi \eta rv=\dfrac{4}{3}\pi {{r}^{3}}\left( {{\rho }_{o}}-\rho \right)g \\
 & v=\dfrac{2{{r}^{2}}\left( {{\rho }_{o}}-\rho \right)g}{9\eta } \\
\end{align}$
The terminal velocity acquired by the ball of radius $r$ when dropped through a liquid of viscosity $\eta$ and density $\rho$ is, $v=\dfrac{2{{r}^{2}}\left( {{\rho }_{o}}-\rho \right)g}{9\eta }$.

Note:Terminal velocity is defined as the maximum velocity attained by a body as it falls through a fluid. It occurs when the sum of the drag force and the buoyancy, or upthrust, is equal to the downward gravitational force acting on the body. Since the net force on the body is zero, the body has zero acceleration. The terminal velocity is directly proportional to the square of the radius of the body and inversely proportional to the coefficient of viscosity of the medium. It also depends upon densities of the body and the medium.