Question

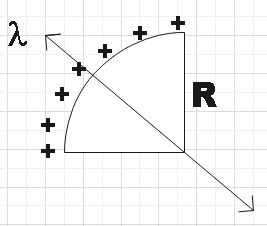
Derive an expression for the electric field at the centre.

Answer 1

Hint: You could firstly consider an arbitrary element from the given quarter circle and then find the electric field due to that small element. On resolving the electric field thus found we understand that we have such components in every one of the small elements in that quarter circle. You could find the net electric components by integrating using appropriate limits for x and y directions and then find their resultant to get the answer.
Formula used:
Electric field,
$\overrightarrow{dE}=k\dfrac{dq}{R}$

Complete answer:
In the question we are given a quarter circle of uniform charge density and are asked to find the net electric field at its centre. We could consider a small element dl that subtends a small angle $d\theta $ at the centre.

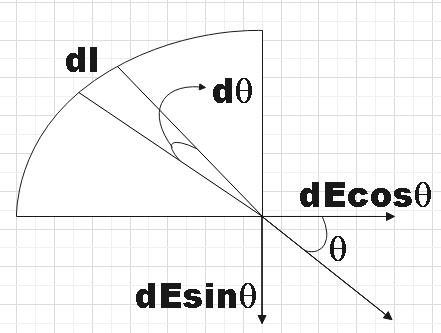
Linear charge density $\lambda $ could be given by,
$\lambda =\dfrac{dq}{dl}$
$\Rightarrow dq=\lambda dl$ ………………………………. (1)
We also have,
$d\theta =\dfrac{dl}{R}$
$\Rightarrow dl=Rd\theta $ ………………………………. (2)
Substituting (2) in (1) we get,
$dq=\lambda Rd\theta $ ………………………………….. (3)
Now the electric field due to this small element under consideration could be given by,
$\overrightarrow{dE}=k\dfrac{dq}{R}$
Substituting (3),
$\overrightarrow{dE}=\dfrac{k\lambda Rd\theta }{{{R}^{2}}}=\dfrac{k\lambda }{R}d\theta $ ……………………………….. (4)
We could resolve $\overrightarrow{dE}$ into its components $dE\cos \theta $ and $dE\sin \theta $
For every small element of the quarter circle will have these components and we have to find the resultant of all these components. Is ${{E}_{x}}=\int{dE\cos \theta }$ and ${{E}_{y}}=\int{dE\sin \theta }$ are the net electric field along x and y directions respectively, then the net electric field due to the given quarter circle would be,
${{\overrightarrow{E}}_{net}}=\sqrt{{{E}_{x}}^{2}+{{E}_{y}}^{2}}$ ……………………………………………… (5)
Now,
${{E}_{x}}=\int{dE\cos \theta }$
From (4),
$\Rightarrow {{E}_{x}}=\int\limits_{0}^{\dfrac{\pi }{2}}{\dfrac{k\lambda }{R}}d\theta \cos \theta =\dfrac{k\lambda }{R}\int\limits_{0}^{\dfrac{\pi }{2}}{\cos \theta d\theta }$
$\Rightarrow {{E}_{x}}=\dfrac{k\lambda }{R}\left[ \sin \theta \right]_{0}^{\dfrac{\pi }{2}}=\dfrac{k\lambda }{R}\left[ 1-0 \right]$
$\Rightarrow {{E}_{x}}=\dfrac{k\lambda }{R}$ …………………………………………… (6)
And,
${{E}_{y}}=\int{dE\sin \theta }$
$\Rightarrow {{E}_{y}}=\int\limits_{0}^{\dfrac{\pi }{2}}{\dfrac{k\lambda }{R}}d\theta \sin \theta =\dfrac{k\lambda }{R}\int\limits_{0}^{\dfrac{\pi }{2}}{\sin \theta d\theta }$
$\Rightarrow {{E}_{y}}=\dfrac{k\lambda }{R}\left[ -\cos \theta \right]_{0}^{\dfrac{\pi }{2}}=\dfrac{k\lambda }{R}\left[ 0-\left( -1 \right) \right]$
$\Rightarrow {{E}_{y}}=\dfrac{k\lambda }{R}$ …………………………………………… (7)
From (6) and (7),
${{E}_{x}}={{E}_{y}}=E=\dfrac{k\lambda }{R}$
Equation (5) now becomes,
${{\overrightarrow{E}}_{net}}=\sqrt{{{E}_{x}}^{2}+{{E}_{y}}^{2}}$
$\Rightarrow {{\overrightarrow{E}}_{net}}=\sqrt{2{{E}^{2}}}=\sqrt{2}E$
$\therefore {{\overrightarrow{E}}_{net}}=\sqrt{2}\dfrac{k\lambda }{R}$
Therefore, we found the electric field at the centre of the quarter circle to be,
${{\overrightarrow{E}}_{net}}=\sqrt{2}\dfrac{k\lambda }{R}$

Note:
You may have noticed the constant that is being used throughout the solution ‘k’. This constant can ‘k’ can be given by,
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}$
Now, we applied limits for the integral from 0 to $\dfrac{\pi }{2}$ as we are performing integration for $d\theta $ and we have applied the limits appropriately for a quarter circle.