Question

Derive an expression for the centripetal acceleration of a body moving with constant speed in a circular path.

Answer 1

Hint: Motion in a circular path means that the angular velocity of the particle undergoing circular motion is constant with time. One should always take care of the difference between scalar and vector quantity. Speed is a scalar quantity and velocity is a vector quantity. If the speed is constant, it doesn’t imply that the acceleration is zero but if the velocity is constant, it always implies that acceleration is zero or motion is non-accelerated.
Formula used:
$a= \dfrac{dv}{dt}$,$v=R \omega$

Complete answer:
To understand the statement mathematically, let’s consider a particle undergoing circular motion with speed ‘v’ and radius ‘R’ on a circular track.
Hence, its angular velocity ‘$\omega$’ will be $\omega = \dfrac{v}{R}$.

Let’s see properly marked diagram from top:

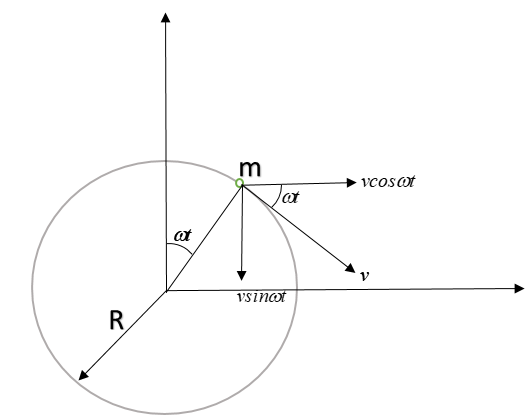
Resolving the speed as velocity into x and y components, so: $\vec { v } =\quad (vcos\omega t\hat { )i } -(vsin\omega t)\hat { j }$
To find the acceleration of the particle, let’s differentiate the velocity expression.
$a= \dfrac{dv}{dt}$
$a= \dfrac{d}{dt}\left ((vcos\omega t\hat { )i} -(vsin\omega t)\hat { j }\right )$
=$v \omega (-sin \omega t) \hat i - v \omega (cos \omega t) \hat j$ $\left ( \dfrac{d}{dt} cos(at+v) =-asin(at+v), \dfrac{d}{dt} sin(at+v) =acos(at+v) \right )$
= $-v \omega (sin \omega t \ \hat i+cos \omega t \ \hat j)$

Putting $v=R \omega$, we get

 $\vec a = -\omega R^2 ( sin \omega t\ \hat i + cos \omega t\ \hat j)$
Hence, vector form of centripetal acceleration is: $\vec a = -\omega R^2 ( sin \omega t\ \hat i + cos \omega t\ \hat j)$ which shows that it’s direction is towards the centre and along the string at every point of circular track.
Expression for centripetal acceleration of a body undergoing circular motion:

As we derived $\vec a = -\omega R^2 ( sin \omega t\ \hat i + cos \omega t\ \hat j)$
To find the magnitude:
$|\vec a| = \omega R^2 \sqrt{(sin \omega t)^2 + (cos \omega t)^2}$=$\omega R^2$ [ $sin^2 \theta + cos^2 \theta = 1$]
Hence centripetal acceleration is $\omega R^2$.

Note:
As we derived the expression for centripetal acceleration of the body undergoing uniform circular motion, we can see that the magnitude of this acceleration is constant with time. One should always remember that whenever a body moves in a curve (basically changes its direction of motion), it will always experience centripetal force acting on it. In short, direction can’t be changed without the application of force. In the above case, the string is providing necessary centripetal force.