Question

What is the derivative graph of a parabola?

Answer 1

Hint: In this problem we need to find the derivative graph of a parabola. For this we will first assume the standard equation of the parabola which is given by $y=a{{x}^{2}}+bx+c$ where $a$, $b$, $c$ are the constants. Now we will differentiate the above equation with respect to the variable $x$. By using the differentiation formula, we will simplify the obtained equation to get the required result.

Complete step-by-step answer:
Let the equation of the parabola will be $y=a{{x}^{2}}+bx+c$.
Differentiating the above equation with respect to $x$, then we will get
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left( a{{x}^{2}}+bx+c \right)$
Applying the differentiation for each term individually, then we will have
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left( a{{x}^{2}} \right)+\dfrac{d}{dx}\left( bx \right)+\dfrac{d}{dx}\left( c \right)$
Taking out the constants from differentiation which are in multiplication with the variables in the above equation, then we will get
$\dfrac{dy}{dx}=a\dfrac{d}{dx}\left( {{x}^{2}} \right)+b\dfrac{d}{dx}\left( x \right)+\dfrac{d}{dx}\left( c \right)$
From the differentiation formula $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$ we can write the value of $\dfrac{d}{dx}\left( {{x}^{2}} \right)$ as $2x$. Substituting this value in the above equation, then we will have
$\dfrac{dy}{dx}=a\left( 2x \right)+b\dfrac{d}{dx}\left( x \right)+\dfrac{d}{dx}\left( c \right)$
We have the value $\dfrac{d}{dx}\left( x \right)=1$. Substituting this value in the above equation, then we will get
$\dfrac{dy}{dx}=a\left( 2x \right)+b\left( 1 \right)+\dfrac{d}{dx}\left( c \right)$
The value $c$ which is in the above equation is a constant. We know that differentiation value of a constant is equals to zero. By using this value, we can write the above equation as
$\dfrac{dy}{dx}=a\left( 2x \right)+b\left( 1 \right)+0$
Simplifying the above equation by using the basic mathematical operations, then we will get
$\dfrac{dy}{dx}=2ax+b$
The equation $2ax+b$ represents the equation of the line. We can observe this in the below graph also

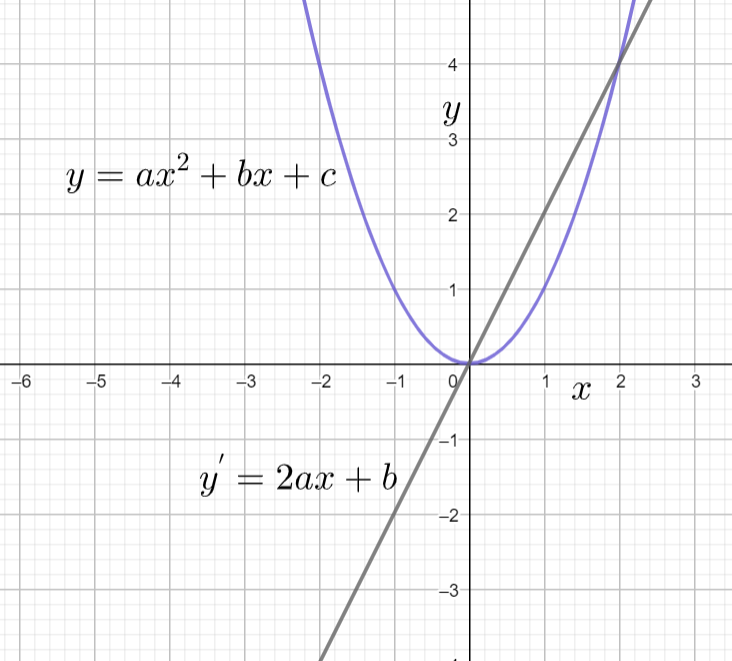
Hence the derivative graph of the parabola is Straight Line.

Note: In this problem we have assumed the equation of the parabola as $y=a{{x}^{2}}+bx+c$ instead of $x=a{{y}^{2}}+by+c$ even though the both the equations represent the parabola. Because the equation $y=a{{x}^{2}}+bx+c$ has an extra advantage to calculate the differentiation value easily over the equation $x=a{{y}^{2}}+by+c$.