Question

Depicted in the plot below is the horizontal force a cube experiences as it slides on a frictionless surface. The force that the cube experiences changes as the function of distance, which is shown on the horizontal axis. What is the work done on the cube from x = 1 m to x = 3 m.
              

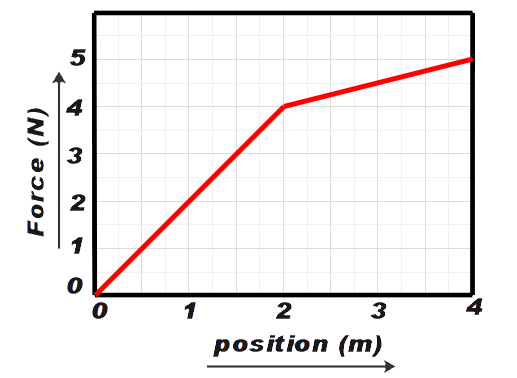
A. 3 J
B. 7.25 J
C. 8 J
D. 4.25 J
E. 7 J

Answer 1

Hint: In this question we have been asked to calculate the work done on the given cube from x = 1 m to x = 3 m. We have been given a force versus position graph. We know that work done is given as the product of force and displacement. But we also know that area under the force-position graph shall always give us the work done on an object, Therefore, we shall find the area under the curve from x = 1 to x = 3.

Complete answer:
We know that area under the Force-position graph gives us the work done on the particle. Therefore, we shall calculate the area under the given graph from x = 1 to x = 3 meters.

           

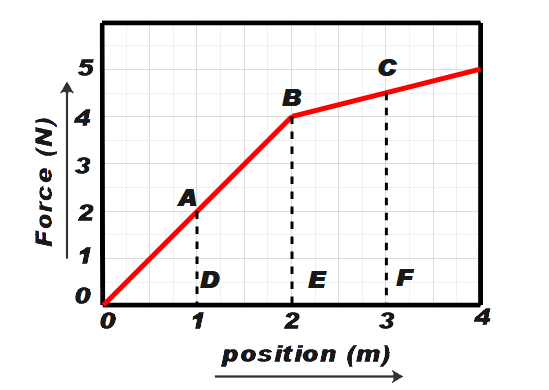
From the figure above we can say that,
AD = 2N, BE = 4N, CF = 4.5N and DE = EF = 1m
Therefore,
We can say that,
Area of trapezium, (DABE) i.e. \[{{A}_{1}}\] can be given by,
\[{{A}_{1}}=\dfrac{1}{2}\left[ AD+BE \right]\times DE\]
After substituting values,
\[{{A}_{1}}=\dfrac{1}{2}\left[ 2+4 \right]\times 1\]
Therefore,
\[{{A}_{1}}=3J\] ………….. (1)
Similarly, area of trapezium, (EBCF) \[{{A}_{2}}\] can be given by,
\[{{A}_{2}}=\dfrac{1}{2}\left[ CF+BE \right]\times EF\]
After substituting given values
\[{{A}_{2}}=\dfrac{1}{2}\left[ 4.5+4 \right]\times 1\]
Therefore
\[{{A}_{2}}=4.25J\] ………….. (2)
Now, we know that for graph of F-x the area under F-x is known as work done
Therefore, work done from x = 1m to x = 3m is given by,
\[W={{A}_{1}}+{{A}_{2}}\]
From (1) and (2)
We get,
\[W=3+4.25\]
Therefore,
\[W=7.25J\]

So, the correct answer is “Option B”.

Note:
When an object is moved or displaced from its initial position to a distance d independent of the path after application of force F, the work done can be given as product of F and distance d. The displacement is caused by the force, therefore, it can be said that work done is the amount of energy required to move an object at distance d.